Arctan

Guitar Outline Equation

y = (A*sin(B*x+C) + D*sin(E*x+F) + G*sin(H*x+I) + J*sin(K*x+L)) * (M + N*x + O*x^2 +P*x^3 + Q*x^4) * atan(R*x) * atan(S*(BL-x))

Home

The Nealon Equation

The Guitars

The Arch Tops

The Classicals

Arctan

The tangent of an angle, α, in a right triangle is the ratio of the length of the opposite side to the adjacent side.

In a Cartesian coordinate system, for an angle measured with respect to the x-axis, the opposite side is the y coordinate and the adjacent side is the x coordinate.

However, any straight line in this coordinate system has the slope Δ y/ Δ x, so the slope is the tangent of the angle.

If the angle is π /2 (90 º ) then the slope is infinite, since Δ x is zero, regardless of the value of Δ y, so the tangent is undefined; in other words, the tangent "blows up" at 90 º .

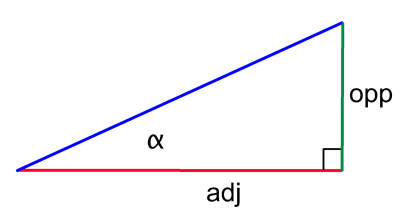
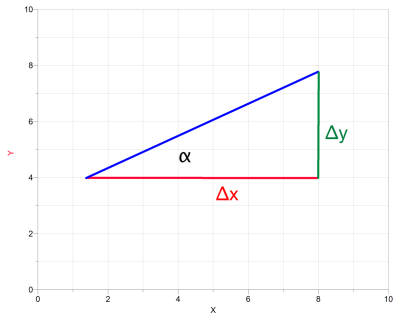
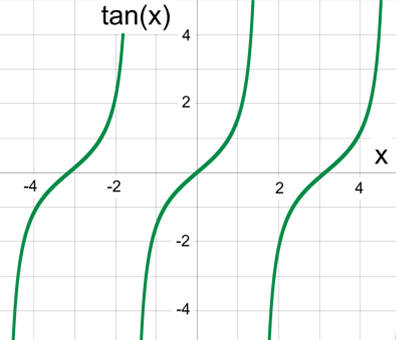
Calculations are in radians, not degrees.

The cotangent is defined as Δ x/ Δ y. For this function, if α = 0, then Δ y is zero and the cotangent blows up; however, the cotangent is defined at 90 º.

The tangent function is periodic over π and goes to infinity at odd multiples of π /2; videlicet, ± 1 π /2, ± 3 π /2, ± 5 π /2, . . . .

Arctangent, sometimes called the inverse tangent, is the angle for a given tangent.

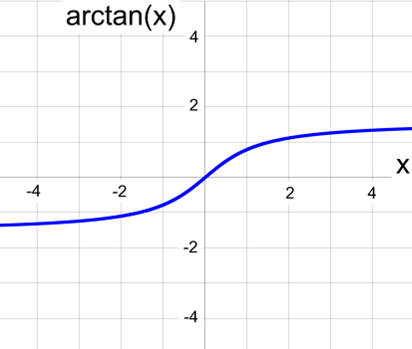
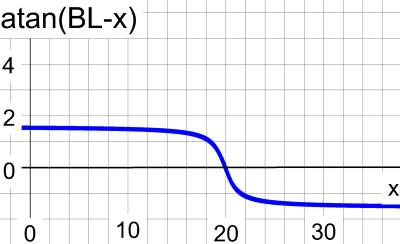
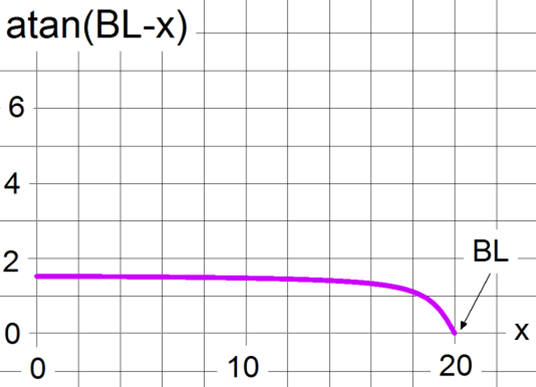
If the tangent of an angle is known (or if the slope of a straight line is known), what angle corresponds to that tangent? Arctangent.

This inverse of the tangent is found by rotating the tangent about an imaginary axis 45 º with respect to the x-axis. The tangent is turned over on its side, so to speak, and it asymptotically approaches π /2 as x goes to infinity.

By writing (BL - x) as the argument, the arctan is offset - and inverted.

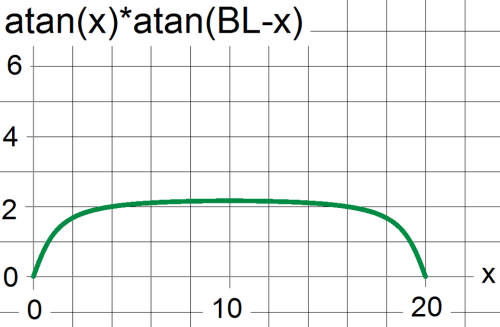
Notice how this arctan term is pinned to the x-axis at the body length, BL. Here I have set BL = 20 and plotted the graph only for 0 < x < BL.

Finally, the product of two arctan terms pins the curve at x = 0 and at BL.
Note the value of the function at the halfway point: at x = 10. If arctan asymptotically approaches π /2, how can the curve be greater than 2 at x = 10? If x = BL/2, then the function graphed here is atan(BL/2 )*atan(BL-BL/2) = 2atan(BL/2).

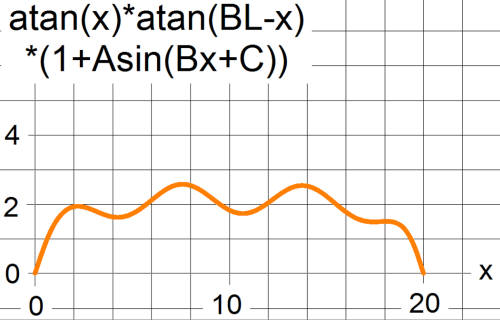
Here is a graph of two arctan terms multiplied by a sin function. The "1+" inside the parentheses is just for the purpose of illustration. For the guitar curve fit there would be a series of sines. The equation for fitting the guitar outline also has a polynomial multiplying the arctans. The constant A is the amplitude, B is the frequency, and C is the phase of the sine. Notice that this equation has only three parameters plus the body length. This example has A = .2, B = 1, and C = .3

Now the curve is starting to look suspicious - but it's just a coincidence. To obtain a perfect fit to a guitar body, at least 19 coefficients are required!

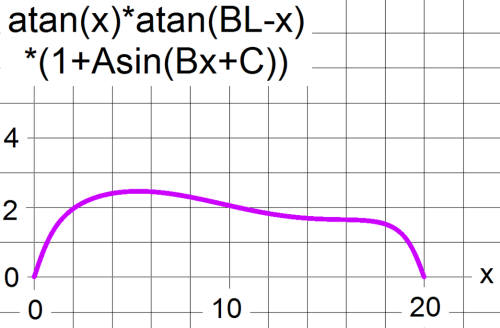
For this curve, A = .2, B = .3, and C = .4