|
The Nealon Equation |
|
y = (A*sin(B*x+C) + D*sin(E*x+F) + G*sin(H*x+I) + J*sin(K*x+L)) * (M + N*x + O*x^2 + P*x^3 + Q*x^4) * atan(R*x) * atan(S*(BL-x)) |
|
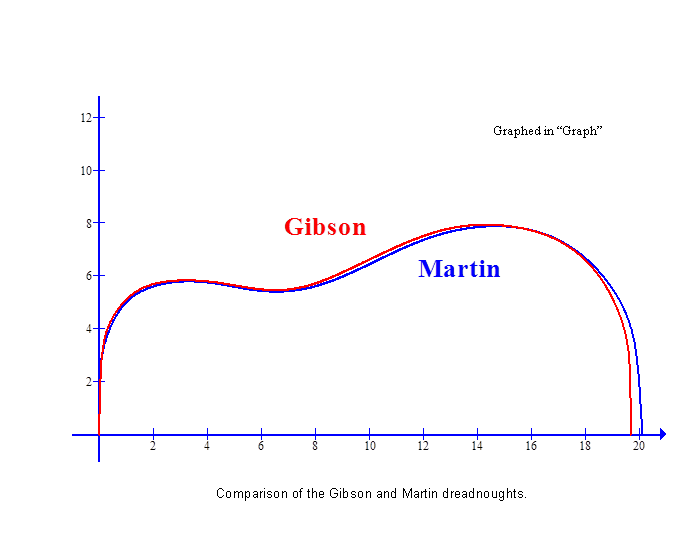
Gibson J40 Dreadnought |
|
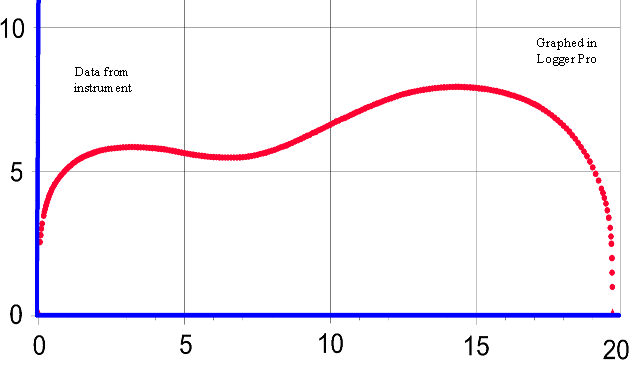
The Gibson dreadnought was laid top-down on a piece of graph paper with 20 lines per inch and aligned along the grid as well as possible. The curve was traced using a half-pencil. Two hundred thirty three data points, shown here, were taken from the paper and then entered into Curve Expert Basic for the curve fit. If you want to try a curve fit to your own instrument you may not need as many points. |
|
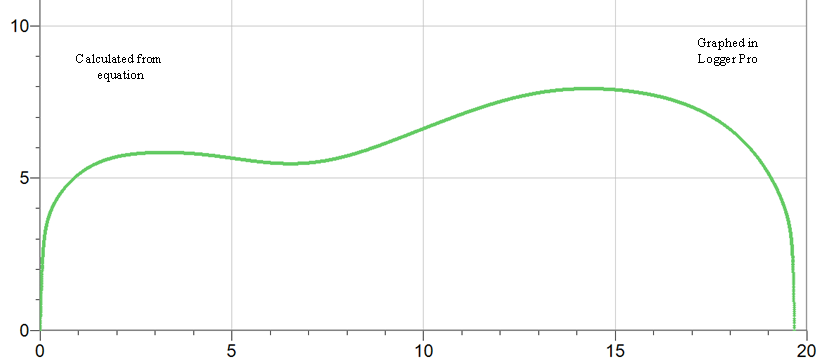
y = (A*sin(B*x+C)+D*sin(E*x+F)+G*sin(H*x+I)+J*sin(K*x+L))*(M+N*x+O*x^2+P*x^3+Q*x^4)*atan(R*x)*atan(S*(19.675-x)) |
|
The coefficients are given with and without the letters in order to be most convenient for use in a variety of graph programs. |

|
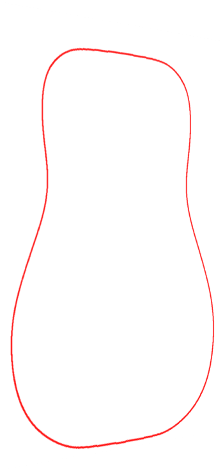
Here the Gibson dreadnought outline was plotted in Graph with the x and y axes deleted. The Graph image was copied (“Copy image” under the “Edit” tab) and pasted twice to a Word document; one of those images was made a mirror image. The two images were then placed side by side - using text wrapping “through” so the images could touch. One way to join the two images into one figure is to capture a screen image - using “Ctrl” and “Print Screen” - then pasting into Paint and cropping away the edges. Now it is one image rotated ninety degrees. Below is the same image using ”3D Rotation” in “Picture Effects” under the “Picture Tools” tab in Word. |

|
Needs new strings. |


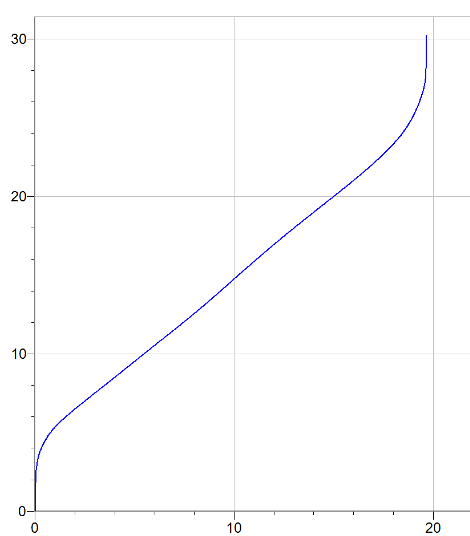
|
Total length of side = 30.24 inches |
|
L |
|
x |
|
Gibson J 40 Dreadnought |
|
|
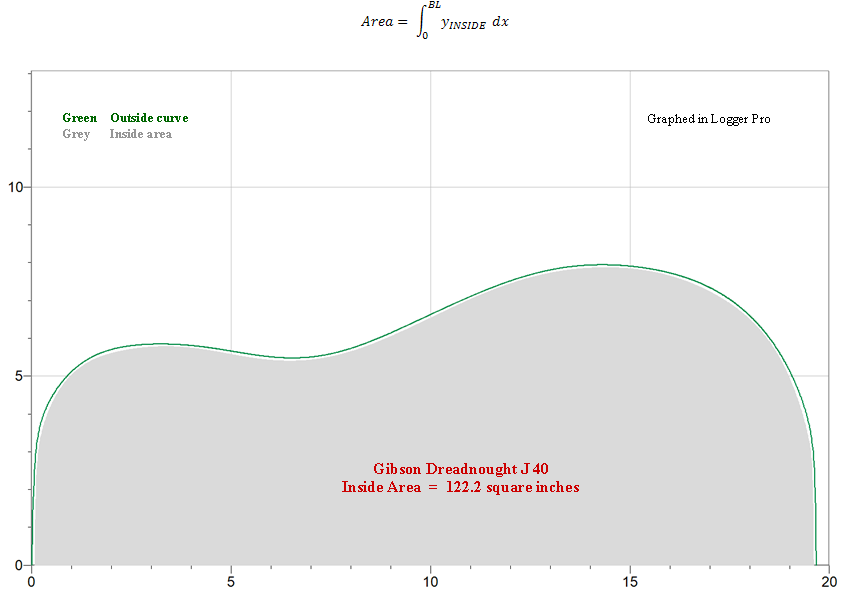

|
Gibson J40 Dreadnought |
|
|
A |
1.185387 |
|
B |
0.3756804 |
|
C |
2.940726 |
|
D |
8.62169 |
|
E |
0.08442539 |
|
F |
-0.5786059 |
|
G |
5.001006 |
|
H |
0.1806989 |
|
I |
1.527422 |
|
J |
0.05155868 |
|
K |
-0.9508379 |
|
L |
-0.1762013 |
|
M |
3.092091 |
|
N |
0.5851531 |
|
O |
-0.1935072 |
|
P |
0.01593922 |
|
Q |
-0.000402921 |
|
R |
21.81638 |
|
S |
34.6247 |
|
BL |
19.675 |
|
|
|
|
A B C D E F G H I J K L M N O P Q R S BL
|
1.185387 0.3756804 2.940726 8.62169 0.08442539 -0.5786059 5.001006 0.1806989 1.527422 0.05155868 -0.9508379 -0.1762013 3.092091 0.5851531 -0.1935072 0.01593922 -0.000402921 21.81638 34.6247 19.675 |
|
|
|
|
A = 1.185387 |
|
|
B = 0.3756804 |
|
|
C = 2.940726 |
|
|
D = 8.62169 |
|
|
E = 0.08442539 |
|
|
F= -0.5786059 |
|
|
G = 5.001006 |
|
|
H = 0.1806989 |
|
|
I = 1.527422 |
|
|
J = 0.05155868 |
|
|
K = -0.9508379 |
|
|
L = -0.1762013 |
|
|
M = 3.092091 |
|
|
N = 0.5851531 |
|
|
O = -0.1935072 |
|
|
P = 0.01593922 |
|
|
Q = -0.000402921 |
|
|
R = 21.81638 |
|
|
S = 34.6247 |
|
|
BL = 19.675 |
|