Volume

The Nealon Equation

The Guitars

The Arch Tops

The Classicals
webpages and Eos image copyright 2015 M Nealon
Air Volume Inside an Acoustic Guitar
The interior of an acoustic guitar body may be divided into four regions for the purpose of calculating the volume of air inside the instrument. The volume bounded only by the sides may be calculated exactly by mathematical formula. Likewise, the two small (almost insignificant) volumes underneath the arched top and back may be calculated. These three volumes added together comprise the interior volume bounded by the wood surfaces of the instrument. Subtracted from that total is the volume taken by all of the interior braces. This, then, gives the volume of air inside the guitar. Let's look at each of the four regions, in turn.
Part I The Rim
The two sides only, but taken together, are referred to as the rim. The edge of the rim which is attached to the guitar top falls on a flat plane. This is the reason that the coordinate system used here, shown in Figure 1, has the top in the x-y plane. The x-axis is along the guitar center line with the origin at the neck. The y-axis describes the body width, and the positive z-axis is the body depth, with the origin at the top of the guitar.
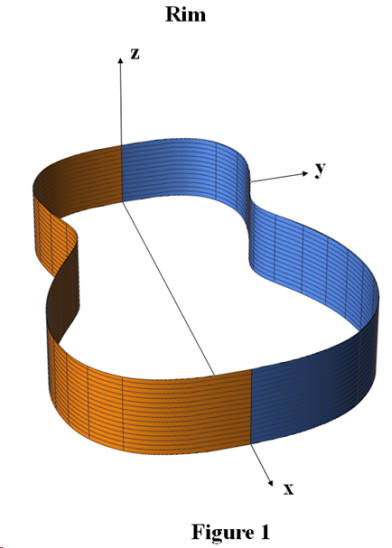
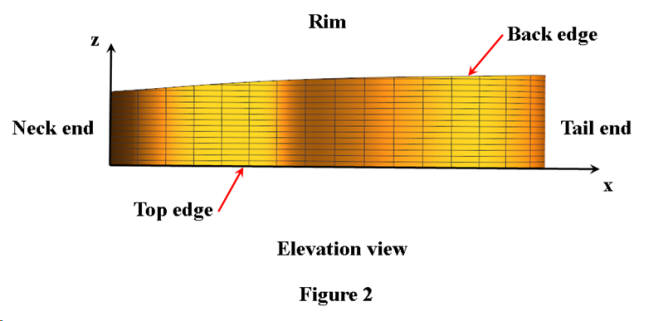
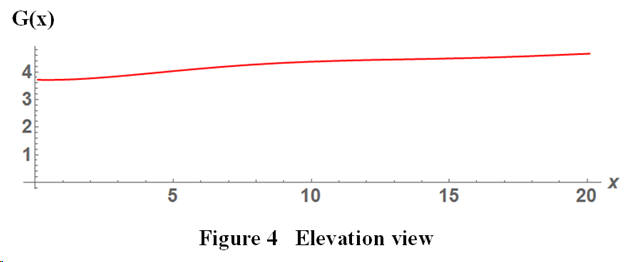
The edge of the rim which is attached to the back is not in a flat plane. A side view of the rim, called the elevation, is shown in Figure 2. Note that the rim height is a measure of the inside dimension of the guitar body. During construction the back and top plates are attached above and below the rim.
Let F(x) describe the body outline in the positive y-direction and create a new variable, x’ , given by
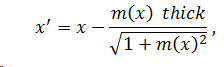
where
thick is the thickness of the side, and
m(x) is the derivative of F(x).
With these, then, the inside edge of the guitar side is outlined by
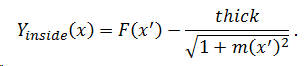
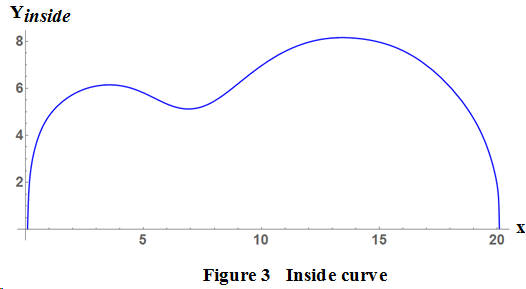
The derivation of this equation is found elsewhere in these pages. This function is shown in Figure 3 for the Fender Jumbo guitar. Note the x-axis offset at the origin by the side thickness, taken here to be a nominal 0.085 inches. The curve is inset by the same amount at the tail end of the instrument. This may not be obvious in the figure, however.
A mathematical description of the elevation is required. Any sort of function will do but a polynomial is convenient. To obtain the rim height the (outside) body height is measured at various x-values. Subtracted from these values are the top plate and back plate thicknesses, assumed to be uniform. Throughout this analysis of volume, all instruments are assumed to have a nominal top and back thickness of 0.1 inch. Typically, a fifth-order polynomial is sufficient to produce a well fit curve; for the Fender Jumbo, this is
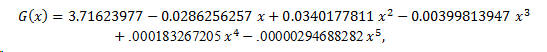
as illustrated in Figure 4. In this figure, as in Figure 3, the curve is plotted for the domain
thick < x < BL-thick ,
where BL is the (outside) body length.
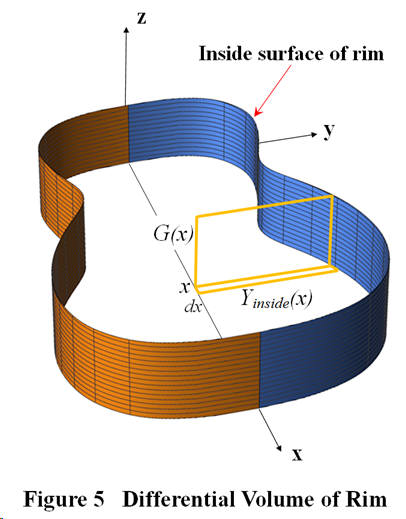
Now for the volume calculation. At any x -value along the center line of the guitar, the product Yinside(x) G(x) gives the rim cross-sectional area, as shown in Figure 5. Multiply that by a differential length, dx , along the x -direction to obtain a differential volume,
A simple matter of a single integration gives the half-volume of the rim as
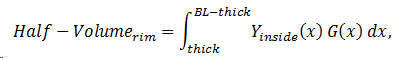
where the limits of the integration in
x
are the inside dimensions of the instrument.
The volume might also be found by triple integral. The differential volume is
dx dy dz
, so the volume is therefore,
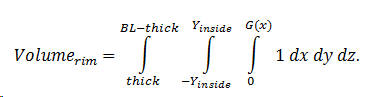
Note that the integrand is given explicitly as 1; Mathematica code requires this.
Part II The Back
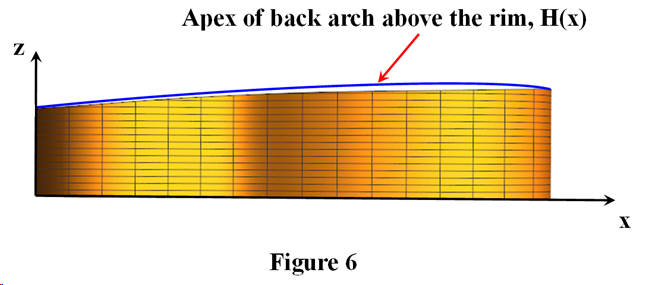
In order to calculate the volume under the slightly arched back an expression, H(x), for the curve along the apex of the arch along the center line is necessary. This is typically written as a polynomial (of any convenient order). For example, this function for the Ibanez Grand Concert guitar is:
Figure 6 illustrates the curve above the rim, but the polynomial written here is without the rim. The curve shown is somewhat exaggerated since the arch is raised above the rim typically less than about 0.1 or 0.15 inches.
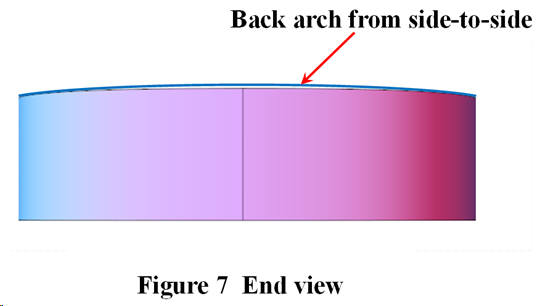
As well as arching from neck to tail, the back arches also from side-to-side, as shown in an end view of an instrument in Figure 7. In order to characterize this side-to-side arch, rather than a polynomial fit to the arch, an appeal is made to the physics of beams. A horizontal beam which is clamped at one end only and which sags under its own weight falls off from the horizontal as the cube of the distance from the clamp. This cube law applies also to beams with added weight.
Guitar top and back plates are braced with quarter-sawn rectangular beams which are, usually, shaped or carved after gluing. One method of attaching these braces is to glue and clamp them into place while the plates placed on a spherically dished board. The plates tend to spring back somewhat from the spherical shape after the glue clamps are removed. I assert that a good approximation for the shape of the side-to-side arch is the cube as described above for the horizontal beam. Written as a function of x and y , we describe the back surface deflection from a flat plane as
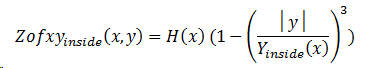
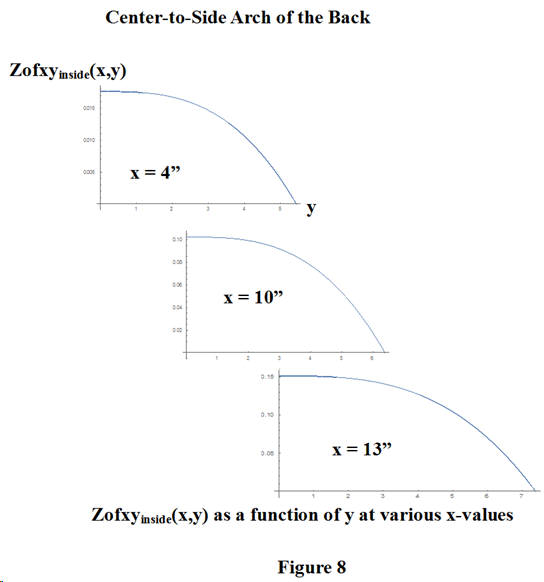
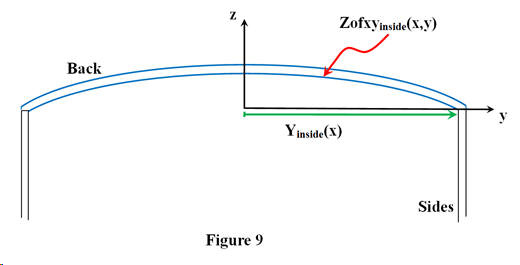
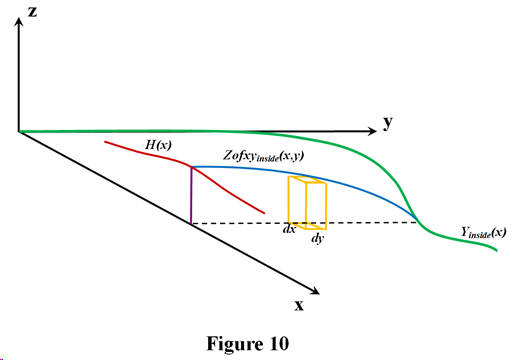
This time, we use a double integral to find the volume under the arched back. See Figure 9 for the cross-section; the x -axis comes out of the page. Since the underside of the back is described by Zofxyinside(x,y) the volume integral is given by
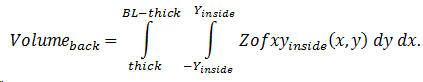
This is an expression for the total volume under the arched back since the limits in the y -direction are from side to side. Figure 10 is an attempt to illustrate, at a given value of x , the scheme for the integration. Multiplying Zofxyinside(x,y) by the area dx dy produces a differential volume, shown by the yellow cuboid in the figure. This differential volume is integrated to give the entire volume under the arched back.
Of course the volume may be determined also by triple integration, as
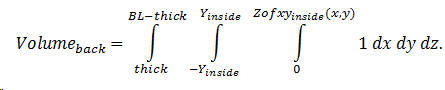
Part IV The Braces
Part III The Top
The volume under the arched top is calculated in just the manner as the back calculation, although the variable names are different in order to avoid confusion. The apex of the top arch along the center line of the guitar is measured and a polynomial is fit. The fourth order polynomial for the Recording King 00, for example, is
The side-to-side arch across the top is the same cube function
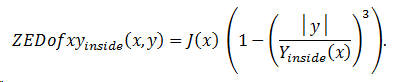
The volume is calculated using both the double and triple integrations.
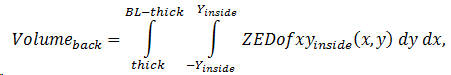
and

Both integrations are performed, just as a check of the results.
Classical
Mitchell 3/4 Size
Fender Jumbo CJ290S