SideUnbending

Side Unbending

y = (A*sin(B*x+C) + D*sin(E*x+F) + G*sin(H*x+I) + J*sin(K*x+L)) * (M + N*x + O*x^2 +P*x^3 + Q*x^4) * atan(R*x) * atan(S*(BL-x))

Home

The Nealon Equation

The Guitars

The Arch Tops

The Classicals

Flattop acoustic guitars are assembled - not carved. There may be a few braces which are carved after being glued on, but in the main, the guitar parts are separately machined, the sides are bent (typically around a hot pipe), and the whole assemblage is glued together in an assortment of (usually hand-made) fixtures and jigs.

Despite the name, the top is not really flat. The top, and for that matter, the back, of an acoustic guitar has a slight outward bow - "out" being defined as the direction away from the interior volume of the instrument. For one thing, a truly flat top plate would look unattractive; specifically, it would look caved in even if it was flat. This must be a trick of the eye in reflected light. However, a slight outward bow in the top and back does serve to add strength against any inward pressures put on these plates. This tends to stiffen the plates, so luthiers should take the amount of this bow into account when preparing the top.

Every guitar maker is free to create a body shape and call it what he will, of course, but there are several commonly used names for the more-or-less standard body styles. Details of the shapes may vary somewhat by manufacturer.

The dreadnought is a loud, large body instrument, with the sound variously described as "full", or "rich", indicating that many overtones are produced over the full scale. These instruments are oftentimes played in a strumming or rhythm style and are found in country, gospel, or folk music bands, among others. Dreadnought sides barely bend in at the waist: about one-half inch or so from the upper bout. This is the most common acoustic guitar sold today.

The orchestra model, OM, or sometimes called 000, has a smaller outline, sharper curves, a more shallow body, and may be described as "brighter" or "more delicate" than the dreadnought and may be more comfortable to hold. Blues players might choose it, for it typically is used with a finger-picking style of play.

The arch-top has a carved top and back, is wider at the lower bout and generally thinner than the other instruments. The arch-top is used in orchestras, where a flat top instrument might be too quiet to be heard. Arch-tops are used in jazz bands as well.

These three types of instruments use steel strings. There are other standard steel string body shapes, such as the 0, 00, or the Jumbo.

The classical guitar is a smaller body instrument which uses plastic strings. These strings have less tension than steel strings so the guitar's top braces need not be quite as strong. There is not much variety in the body shape of classical guitars.

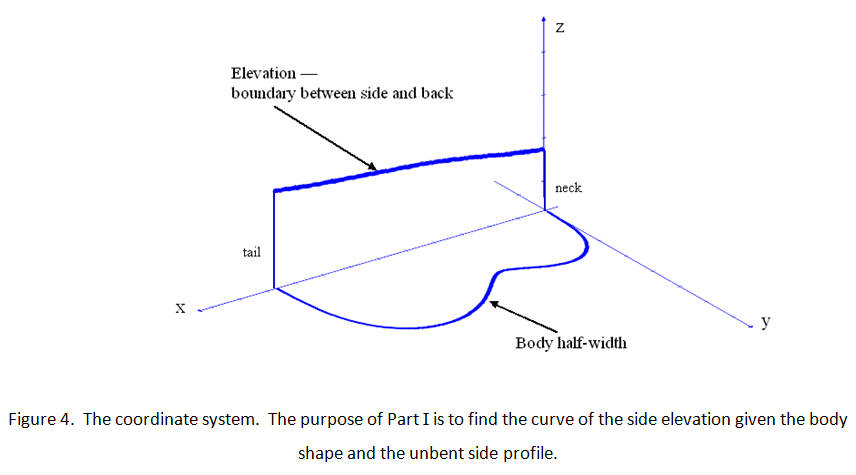
Some guitar designers use French curves, compasses, T-squares and triangles when a full scale drawing is required. Generally, the large body instruments can be outlined with three circular arcs and straight lines; the smaller instruments, with their more sinuous curves might require a few more arcs. Some drafting programs easily deal with arcs, such as the Bezier technique of drawing curves, so an outline may be laid out piece by piece on a computer without too much difficulty.

Acoustic guitar blueprints sometimes include a side view, or elevation, of the completed guitar as shown in Figure 1, although usually not with the neck attached, as illustrated here. From this point of view the bent nature of the side is not noticeable. The boundary between the back and side looks like a broad arching curve stretching from the neck block to the tail block. The apex of the arched back is, of course, a different, higher curve in the elevation view, but this particular curve is of no concern at the moment.

Not all blueprints, however, include the more useful profile of the unbent side, as shown in Figure 2. Unbent sides have that low, very elongated "s" shaped curve along the edge which joins the back. The edge which joins the top is a straight line. In making a template for profiling the unbent side, the question arises: given only the side elevation of the guitar, What should the unbent side look like? Likewise, the question could be posed the other way around: given the shape of the unbent side, What will the side elevation of the completed instrument look like?

The formulation given below will answer those questions, and well as answer yet another question: Where along the "s" curve of the unbent side does the guitar waist occur? These questions are addressed using Monsieur Grellier's blueprint of a 1940 Gibson L-00 (http://grellier.fr/plans.php?lang=fr) and the C. F. Martin and Company's dreadnought blueprint. These two blueprints will be useful because they each include both the side elevation and the unbent side profile. Given both views, the answers to these questions can be checked against the blueprints - with the presumption, of course, that the draftsmen were conscientious in their accuracy.

Part I

Given only the unbent side profile,
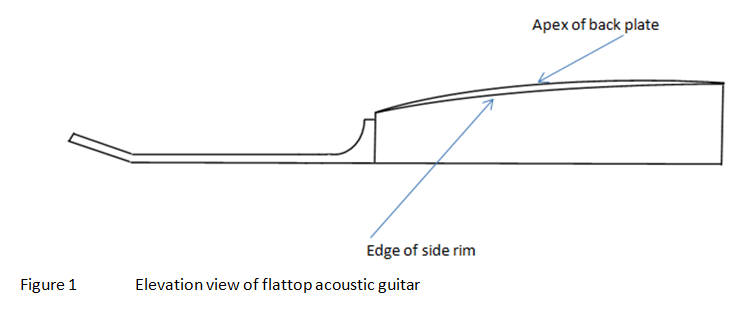
what does the side elevation of the completed instrument look like?

Using Grellier's Blueprint of a 1940 Gibson L-00 Guitar

Naturally, any solution to the problem will require a mathematical model for the unbent side profile. Figure 3 shows data for the unbent profile of Grellier’s Gibson L-00 taken from his blueprint.

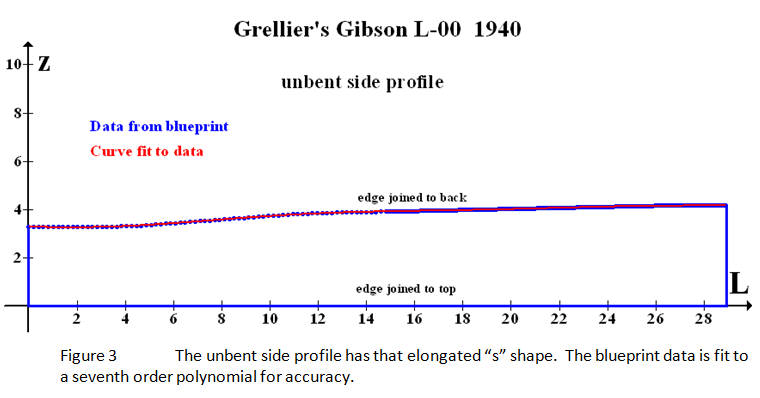
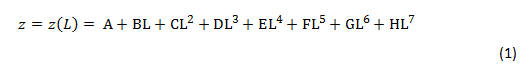
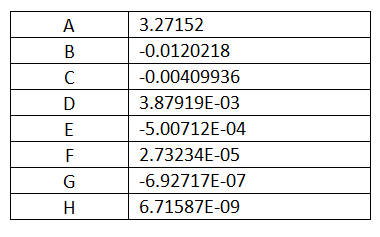
where the letters A through H are coefficients for finding the best fit. This polynomial gives a very close fit to the data. Such a close fit is necessary if the calculated elevation is to match the subtle curves of the figure in the blueprint. Notice from the formula that if L = 0, then z = A. This is the side height at the neck. This formula could be used to print a full size plan for the unbent side, given the coefficients. Curve Expert Pro - the curve fitting program - gives the coefficients for Grellier's Gibson L-00 as:

The z-axis is defined as the direction along the side height; the straight edge which will join the top is along the length, or L-axis. The data for the side height is fit with the seventh order polynomial

Figure 4 shows the coordinate system. The x-axis is along the guitar centerline, with x=0 at the neck. The y-axis is in the plane of the top plate and represents the body half-width. Values along the z-axis, then, give the body depth - meaning the height of the side rim only. A mathematical formula which describes the elevation curve shown in the figure is the object of Part I. Once found, this formula will give the body depth at all points along the center line of the guitar - ignoring any arch or bow in the back.

This body depth is found by correlating the x-axis to the L-axis. The connection between the two axes is the path length along the bent side. This path length is found using the scheme described somewhere in these pages using the function, y(x), for the body outline. Somewhere else around here you can find the parameters for the body outline of the L-00. Once the formula for the body outline is known, then the path length is

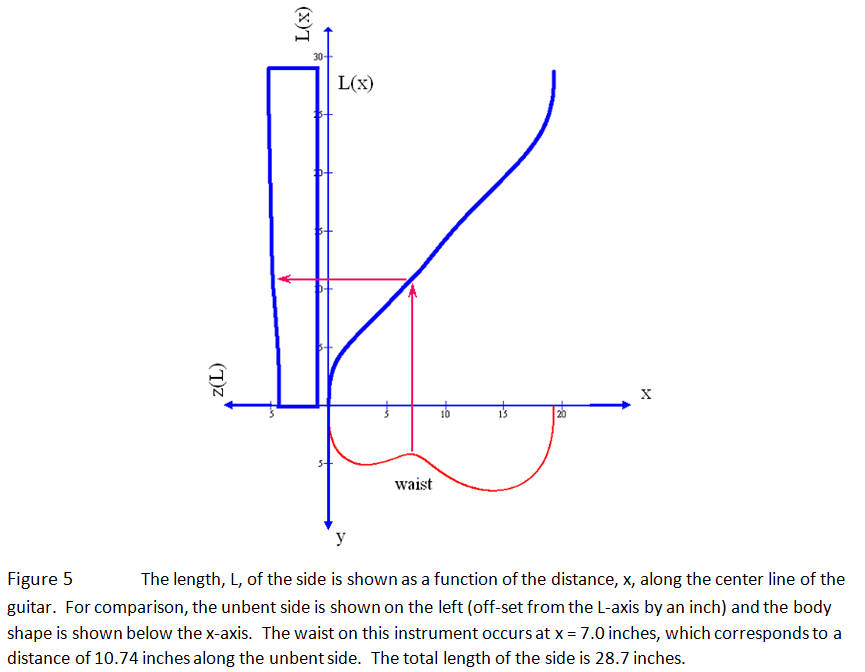
is the derivative of y(x). For any point x, this equation gives the distance along the length of the side up to that point, as shown in Figure 5.

where

Now, all that is left to do is substitute equation (2) into equation (1) to find an expression for the side height as a function of x. The computer does the calculation easily and voilà: Figure 6. This calculated side elevation can be checked against the elevation drawing given in the blueprint. The side elevation in the blueprint shows what the outside of the instrument will look like so it includes the thickness of the back (25.5mm = 0.098") and the top (2.8mm = 0.11"). Correcting for this is a simple matter of subtraction, assuming a uniform thickness of the plates, which gives the height of the side alone. It is apparent in Figure 6 that the calculated curve follows the subtle curvature of the data quite well.

Now let's go backwards.

Part II

Given only the side elevation,
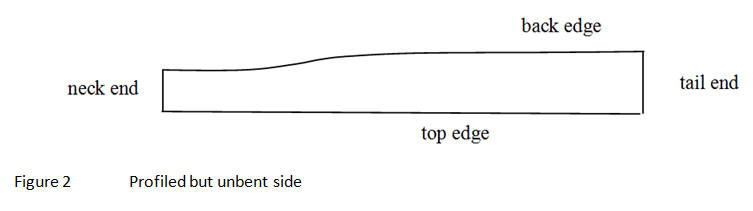
what does the unbent side profile look like?

Using Martin's Blueprint of a Dreadnought Guitar

This time the (seemingly-no-longer-available) Martin dreadnought blueprint is used. The first step is to use Curve Expert Pro to fit a curve to the body outline, y(x), which is required for the solution of equation (2). The body outline and length are shown in Figure 7.

The next step is to fit a curve to the side elevation. The elevation at the neck is given as 3 7/8 inches. The Martin blueprint specifies that the top thickness be a uniform 0.1" and the back be 3/32". The drawing includes these, so the data shown in Figure 8 are corrected for these plate thicknesses. This gives the side height at the neck as 3.68 inches. The curve in Figure 8 is an expression of z as a function of x. Any good equation will do, but a fit to the curve is obtained here with a fifth order polynomial. Remember, an excellent fit now will help in producing the best results in the solution.

In order to make the path to a solution clear let us now review what we have to this point and what we are after. Equation (3) gives z, the body height, as a function of x, the distance along the center line of the guitar; equation (2) gives L, the unbent side length, as a function of x. What is required is z as a function of L.

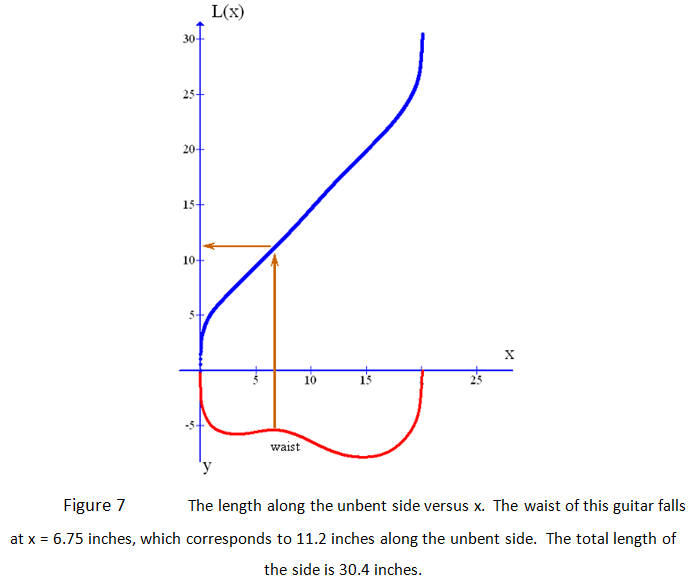
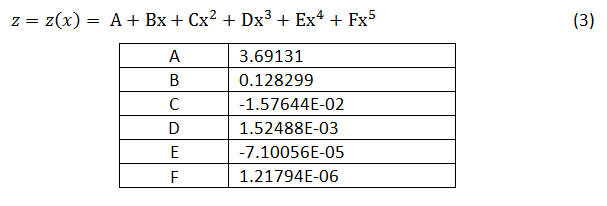
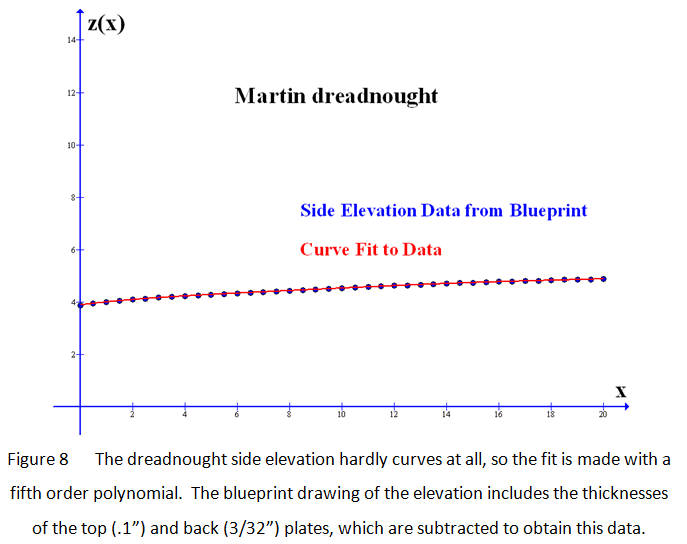
The solution of equation (3) is exact and equation (2) is solved numerically in a graphing program. The straightforward solution to the overall problem would be to find an exact solution to equation (2) by taking the derivative of y(x), performing the integral and using the rules of algebra to rearrange it as an expression for x as a function of L. Then substitute that expression for x(L) into equation (3) for the exact solution z(L). All of this - even if possible - is completely unnecessary, since the problem is already solved!

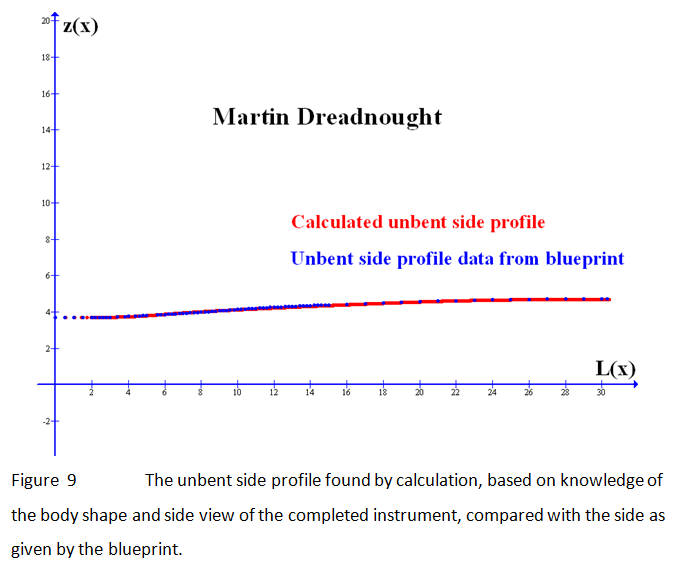
Equations (2) and (3) are a parametric representation of the relation between z and L, with the variable x acting as the parameter. The values over which the parameter ranges are its domain: 0<x<BL, where BL is the body length. Since L(x) and z(x) are already solved over the domain of x, simply make a graph of the Cartesian coordinates (L(x),z(x)) for all x within its domain.

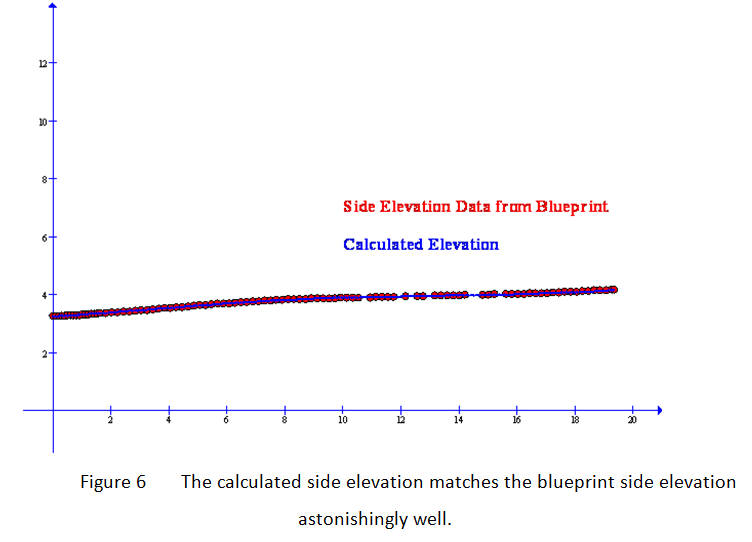
This solution is shown in Figure 9 along with the data points of the unbent side from the Martin blueprint. The drawing of the unbent side has no scale, so the height at the neck is taken to be 3.68 inches. Again, the correlation between the calculation and the data is quite close, indicating that the formulation given here should be, for those blueprints which do not have a side profile, a useful method of "unbending" the sides.

The End