|
y = (A*sin(B*x+C)+D*sin(E*x+F)+G*sin(H*x+I)+J*sin(K*x+L))*(M+N*x+O*x^2+P*x^3+Q*x^4)*atan(R*x)*atan(S*(20.09-x)) |
|
The Nealon Equation |
|
y = (A*sin(B*x+C) + D*sin(E*x+F) + G*sin(H*x+I) + J*sin(K*x+L)) * (M + N*x + O*x^2 + P*x^3 + Q*x^4) * atan(R*x) * atan(S*(BL-x)) |
|
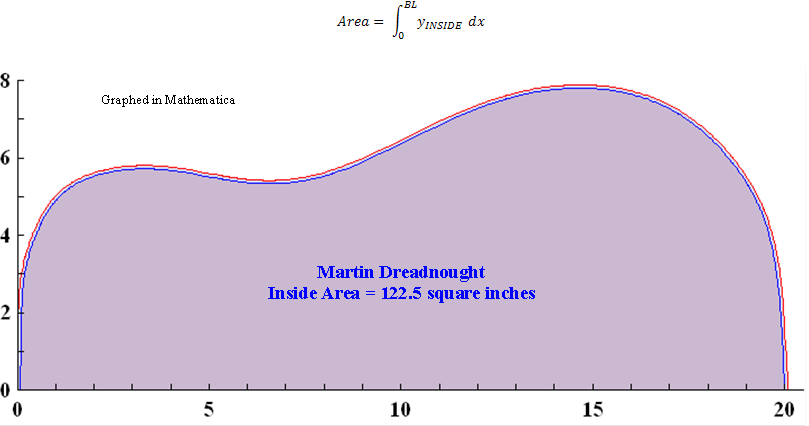
Martin Dreadnought |
|
“The dimensions in this drafting are not necessarily the historical or current specifications of any Martin model.”
“White plastic strap button”
- quotes from the blueprint. |
|
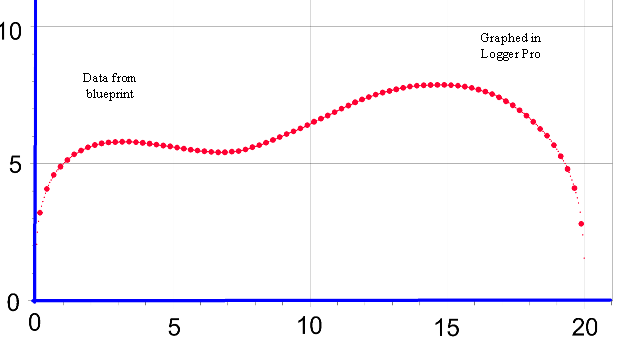
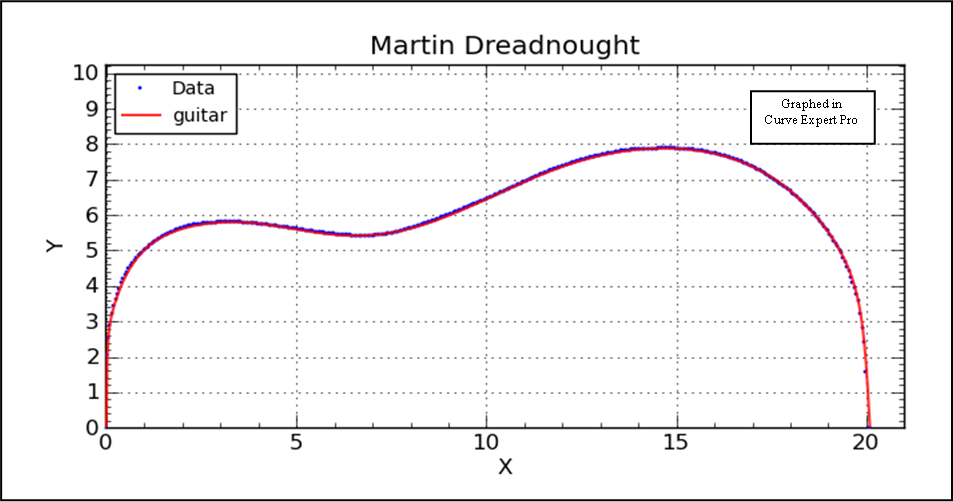
The red line is the curve given by the equation and is plotted with 1000 points along the x-axis. The blue dots are the same data as above. Pretty close fit, huh? These coefficients in the tables come from the latest fit using Curve Expert Pro. Curve Expert Pro calculates the numbers to 15 digits. Consider at least 7 to be significant - meaning that, if you make a graph with these numbers you should use at least 7 digits. Both tables have the same set of numbers. You can copy and paste the equation or coefficients into your programs. In some graph programs you will need the numbers without the letters. In some curve fit programs you may need the letters and equal signs. Be sure not to overlook the negative signs when copying. It might be better to keep the letters case specific. |
|
This graph shows 403 data points which are used for curve fitting. The body length is 20.09”, and yes, there are points at (0,0) and (20.09, 0); they’re just hidden by the blue axis. Not all data points have the big red circle. |
|
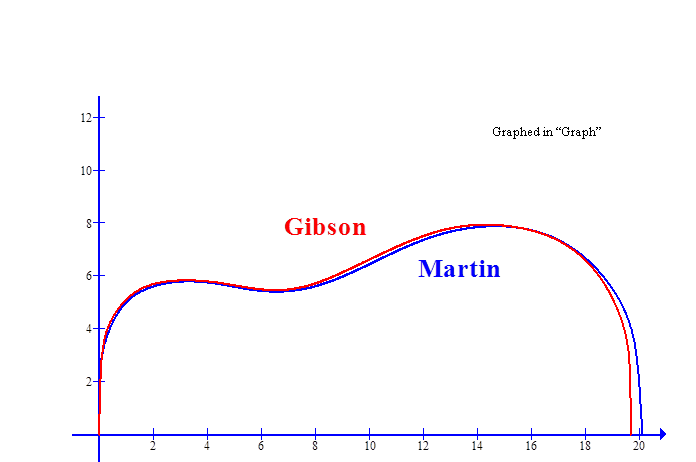
Comparison of the Gibson and Martin dreadnoughts. |

|
|
|
Graphed in Mathematica |
|
L |
|
x |
|
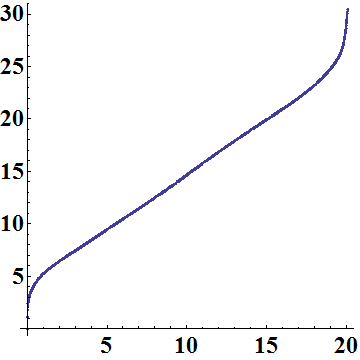
The length of the side calculated using the Mathematica program with the formula given alongside, drawn as a function of x. The program will actually figure out the derivative, dy/dx, explicitly. Total side length is calculated to be 30.45 inches, |


|
Martin Dreadnought |
|
-1.20396985751850E+03 -4.04924543227359E-01 1.67178639052132E+00 -1.41568846803447E+03 3.66260076357758E-01 -1.47955747238546E+00 6.72101651604178E+02 -3.37320036709983E-01 4.48184137133363E+00 -4.54587164058976E+02 4.30257674959261E-01 1.07644053151715E+01 8.34056674609041E+00 -1.68976474587851E+00 1.32668991106339E-01 -4.73588903287060E-03 6.46082606066693E-05 7.11597279858213E+01 7.08177622702534E+00 |
|
BL = 20.09 |
|
Martin Dreadnought |
|
A = -1.20396985751850E+03 B = -4.04924543227359E-01 C = 1.67178639052132E+00 D = -1.41568846803447E+03 E = 3.66260076357758E-01 F = -1.47955747238546E+00 G = 6.72101651604178E+02 H = -3.37320036709983E-01 I = 4.48184137133363E+00 J = -4.54587164058976E+02 K = 4.30257674959261E-01 L = 1.07644053151715E+01 M = 8.34056674609041E+00 N = -1.68976474587851E+00 O = 1.32668991106339E-01 P = -4.73588903287060E-03 Q = 6.46082606066693E-05 R = 7.11597279858213E+01 S = 7.08177622702534E+00 |
|
BL = 20.09 |