|
The Nealon Equation |
|
y = (A*sin(B*x+C) + D*sin(E*x+F) + G*sin(H*x+I) + J*sin(K*x+L)) * (M + N*x + O*x^2 + P*x^3 + Q*x^4) * atan(R*x) * atan(S*(BL-x)) |
|
Concert Acoustic 12-Fret |

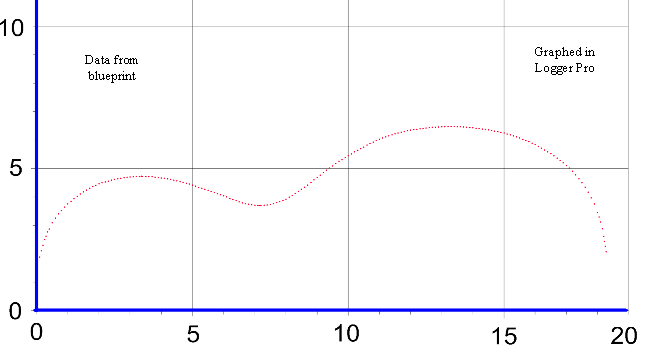
|
y = (A*sin(B*x+C)+D*sin(E*x+F)+G*sin(H*x+I)+J*sin(K*x+L))*(M+N*x+O*x^2+P*x^3+Q*x^4)*atan(R*x)*atan(S*(18.375-x)) |
|
These coefficients come from the latest fit (later than the American Lutherie article) using Curve Expert Basic. The Logger Pro graph is plotted with 3676 points along the x-axis. Both tables give the same numbers. In some graph programs you will need the numbers without the letters. In some curve fit programs you may need the letters and equal signs. Be sure not to overlook the negative signs when copying. |
|
This graph shows 194 data points which are used for curve fitting, and yes, there are points at (0,0) and (18.375, 0); they’re just hidden by the blue axis. |
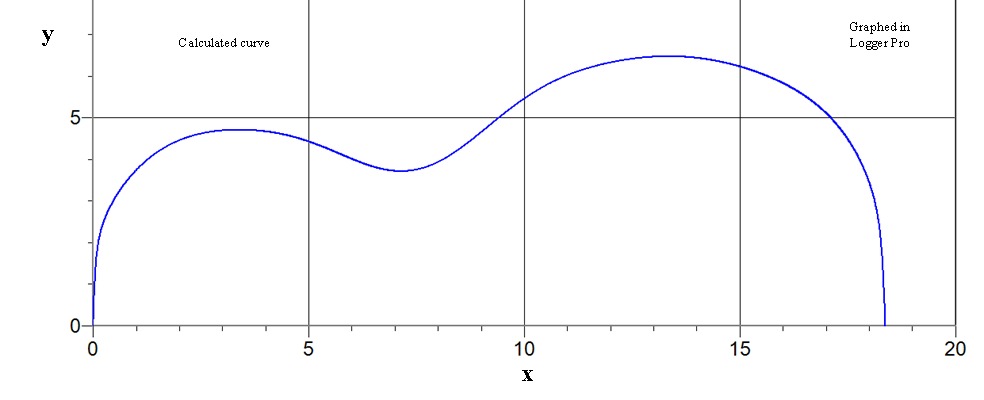
|
An old blueprint from ILS. Open string length 24.75“ |
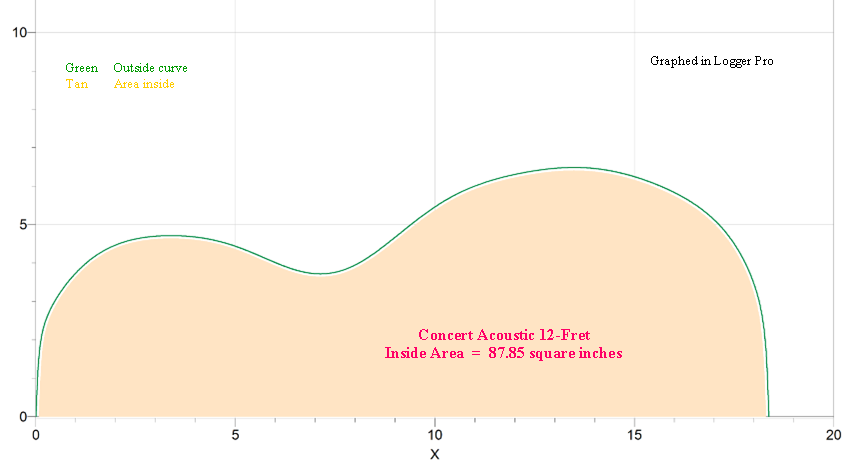
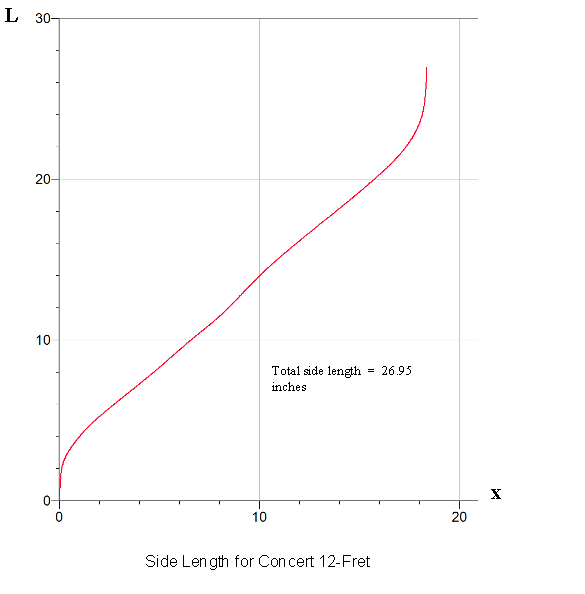

|
|
|
Concert Acoustic 12-Fret |
|
A = 1.99513644375E+000 B = 4.76767017283E-001 C = 1.35471273105E+000 D = -3.45840481752E+000 E = 2.94232476246E-001 F = -1.67468328664E+000 G = 7.69541908551E+000 H = -1.94517727658E-001 I = 3.62586382730E+000 J = 7.21647719099E-002 K = 1.39808846599E+000 L = 4.29289713865E-001 M = 5.37031397224E-001 N = -6.94366368501E-002 O = 2.73882758490E-002 P = -3.04419197770E-003 Q = 1.00788967324E-004 R = 1.95704229874E+001 S = 1.42773734153E+001 |
|
BL = 18.375 |
|
Concert Acoustic 12-Fret |
|
1.99513644375E+000 4.76767017283E-001 1.35471273105E+000 -3.45840481752E+000 2.94232476246E-001 -1.67468328664E+000 7.69541908551E+000 -1.94517727658E-001 3.62586382730E+000 7.21647719099E-002 1.39808846599E+000 4.29289713865E-001 5.37031397224E-001 -6.94366368501E-002 2.73882758490E-002 -3.04419197770E-003 1.00788967324E-004 1.95704229874E+001 1.42773734153E+001 |
|
BL = 18.375 |