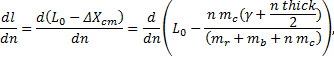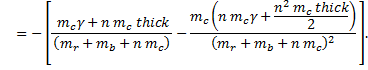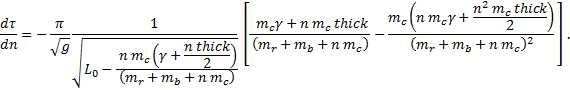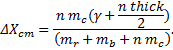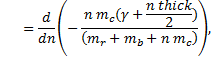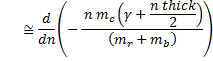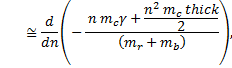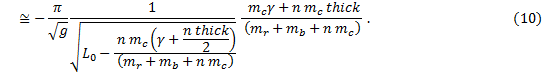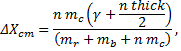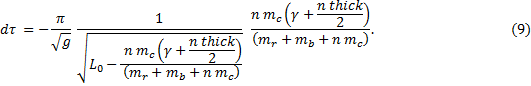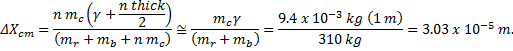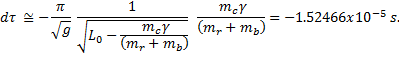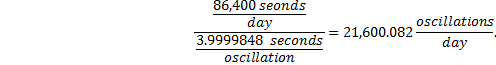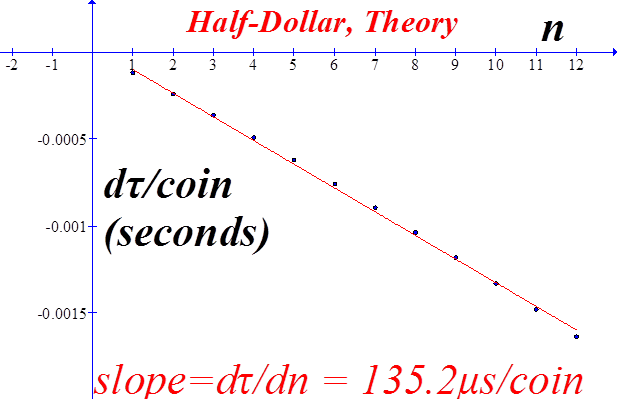PHYSICS HOME

The Pendulum

HOME

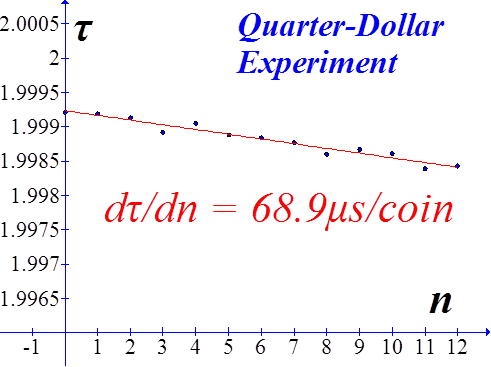
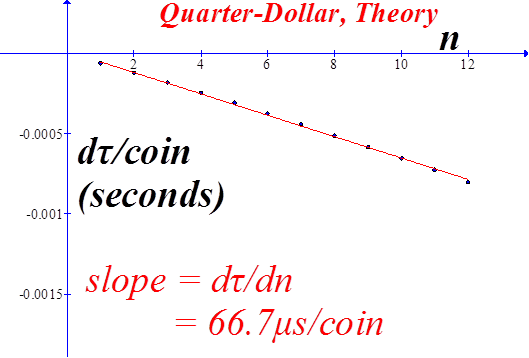
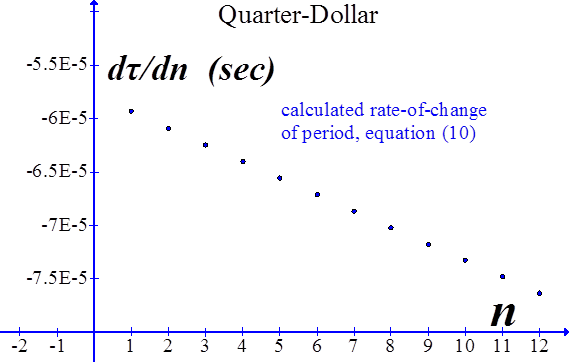
B         US Quarter-Dollar

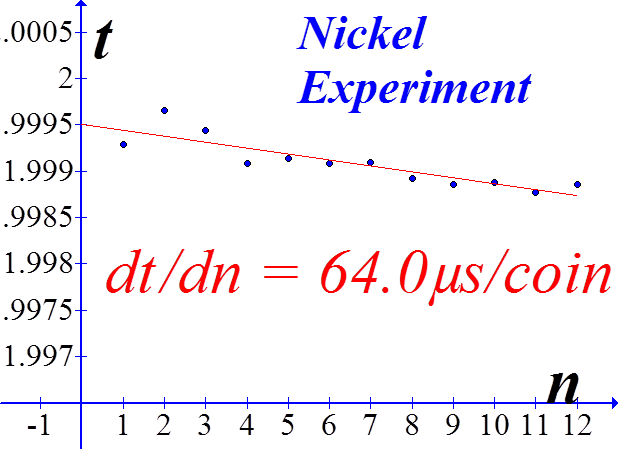
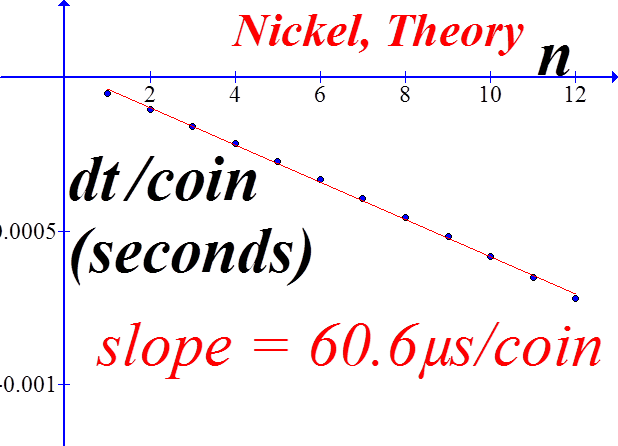
C         US Nickel

 

 

Equation (9) requires the pendulum length, L_0, with no coins on the bob.  In order to find that value, we extrapolated sonic data B values to find B₀ and consequently L₀.  Here, however, we are interested only in the slope of (9) with respect to n.

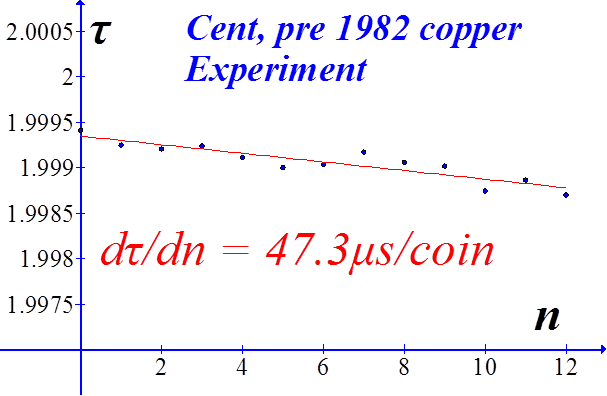
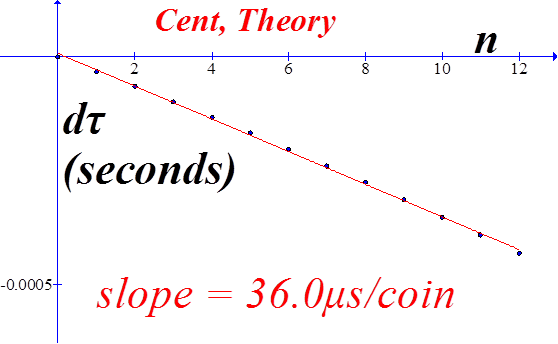
D        US Cent, pre 1982 copper

 

Theory 3.     Taking the full derivative.

 

For this derivative, we need the product rule.  Remembering that L₀ has no dependence on n,

 

Now dτ/dn,

 

The difference between this theory and Theory 2 is negligible.

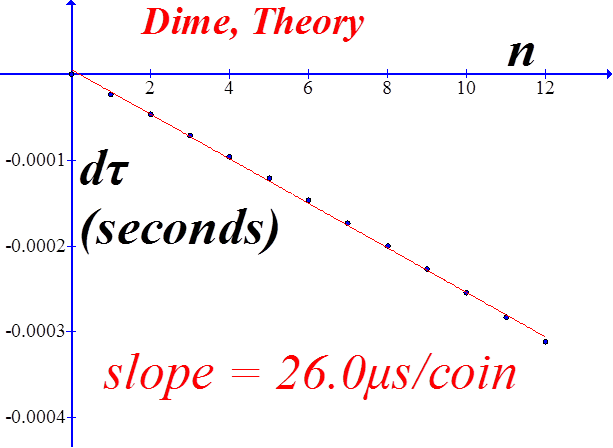
E         US Dime

Theory 2.     Using an approximation for the total mass in the derivative.

 

The change in the length of the pendulum due to the addition of coins, as mentioned above, is

 

The denominator in this expression is the total mass of the pendulum (ignoring, of course, the masses of the 1” spring steel, the brass sleeve, the rating nut and the magnet); this includes the masses of the rod, the pendulum bob and the coins.  The total mass of the coins placed on the top of the bob depends on the number of coins, of course.

 

The largest coin used in this analysis is the US half-dollar, which has a mass of 0.011340 kg and the maximum number of coins is 12; therefore, even the maximum mass of coins (0.136 kg) which might be used to regulate the pendulum rate is small compared to the sum of the masses of the rod and bob (6.189 kg).  Thus, the mass of the coins may be ignored. 

 

The purpose of ignoring the mass of the coins is to remove any dependence on n in the denominator.  Taking the derivative will be a much more manageable task.

 

L₀ has no dependence on n, so

 

Taking the derivative gives us

 

where we have restored the total mass in the denominator after taking the derivative.

 

Finally, we have

 

Note that equation (10) calculates dτ/dn directly and that it is a function of n.  Notice also that (10) does not have an n² term, unlike equation (9). 

 

 

 

 

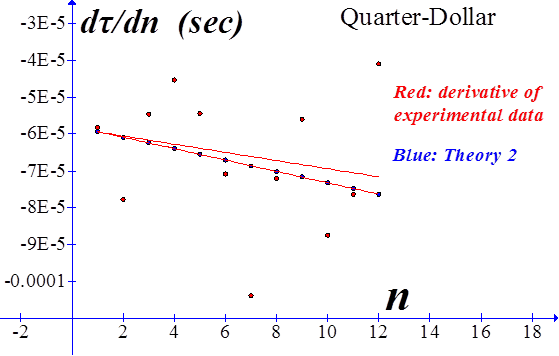
An attempt to compare the theory, equation (10) with measured data.  The slope of the best fit line to the derivative of the measured data (red line) is -5.2x10^-6 sec, and the slope of the theoretical rate-of-change is -3.7x10^-6 sec.  Not a bad comparison.

Comparison of the theory with experimental data for quarters.  Interestingly enough, the slope of theoretical prediction doesn’t deviate too much from the best fit line to the experimental data, despite the scatter in the data.

We will leave it to the reader to determine the answer to this question:  If more than one coin is required, is it more effective to stack the pennies, or arrange them side-by-side on the top of the bob?

Great Clock in the Tower at the British Houses of Parliament

 

The clock pendulum is 4.4 m (about 14 feet) long and has a mass of 310 kg (682 lb).  The four-second period is said to have a “2 second beat”.  The pendulum bob mass is 203 kg (447 lb), so presumable the rod and support mechanism for the bob must have a mass of 107 kg (235 lb).  The bob consists of concentric tubes of steel and zinc.

 

We have no data on the size of the bob, but an estimate from the above photograph of the height of the bob is 20” (.5 m) and diameter is 16” (.4 m). 

 

 

  

Great Clock

 

This photo, taken from a 1959 Pathé newsreel, shows Mr. Charles King placing a coin on the shoulder of a bracket on the pendulum rod.   From the Houses of Parliament website:

 

                 “Pendulum adjustment: pre-decimal pennies are used to regulate the clock mechanism. Adding one penny causes the clock to gain two-fifths of a second in 24 hours.”

 

The coins used for regulating the period are solid bronze pre-decimal British pence coins.

Estimate of British Pre-decimal Bronze Pence Coin Thickness

Density of bronze:      Bronze (8-14% Sn)           7400 – 8900 kg/m³

Density values depend on amount of tin in the alloy.  The density for 8% to 14% tin ranges from 7400 kg/m³ to 8900 kg/m³.  Pre-decimal British pence coins have between 0.5 and 4% tin, so the lowest value is probably the best estimate to take in order to estimate the thickness of the coin.  Write an expression for the volume,

or,

Data for the coin:

mass = 9.4x10^-3 kg

diameter = 3.1x10^-2 m;

therefore,

r = 1.55x10^-2m

and

thick = 9.4x10^-3 kg/( 7400kg/m³ π [1.55x10^-2 m]² ) = 1.68 mm.

 

Obverse       Reverse

 

 

 

This wide shelf where the pence coins are placed to regulate the rate is the “shoulder” of the pendulum.

 

Using the diameter, 1.25”, of the pence coin as a scale, we estimate from the photo:

The long rod (4.4 m long) at the top of the photo: about 1” diameter.

The bob support (with holes) at the bottom of the photo: about 3” diameter.

 

Equation (9) gives an expression for the change in period per coin for the regulation of a pendulum clock by the addition of coins on the bob.  If the great clock at the British Houses of Parliament has a nominal period τ = 4 seconds, then the effective length, which is the true center of mass, must be

 

An inspection of the Pathé newsreel and the photograph of Mr. King placing the coin on the pendulum will reveal that the shelf on which the coins rest is well above the top of the bob.  The bob is below the floor.  Lacking any information, a rough order of magnitude, then, is the best guess for the distance above the center of mass where the coins reside.  We have referred to the distance from the true center-of-mass to the coin as γ.  So let us make the assumption that this distance is nominally γ = 1 meter.  From the discussion of theory 2, we have

 

and

 

For the great clock pendulum, we know that m_r + m_b = 310 kg, and for a pre-decimal pence coin, m_c = 9.4 x10^-3 kg.  We assume γ >> thick/2, so for a single coin,

 

Therefore, the period changes by an amount

 

The period with one coin would therefore be 4 s -1.52466x10^-5 s = 3.9999848 s.  This pendulum would oscillate

 

Since a properly adjusted pendulum would oscillate 21,600 times per day, the pendulum has 0.082 extra oscillations.  This pendulum would be “fast” about 0.33 seconds per day, corresponding to about 1/3 seconds per day.  As a rough estimate, this compares favorably to the value reported by the Parliament website of two-fifths of a second in 24 hours.

Data and Theory for Rate-of-Change of Period

 

Equation (9) is the simplest approximation for the rate-of-change of the period.  This equation is plotted here for each of the coin dominations, and for comparison, the slope of the experimental data.

 

///////////////////////////////////////////////////////////////////////////////

 

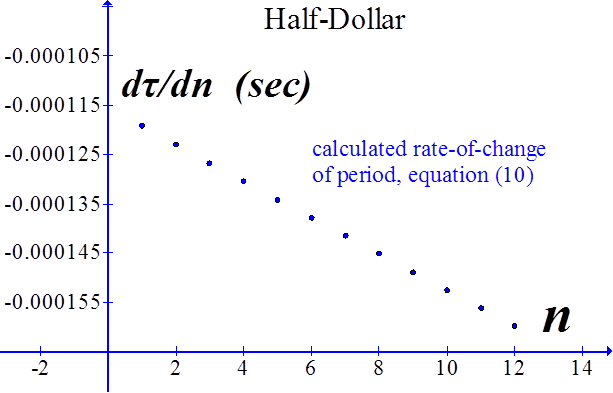
A        US Half-Dollar

Sonic detector data converted to period. The slope is the rate-of-change of the period with respect to the number of coins.

 

Plot of equation (9) for half-dollars.  The slope of the dτ vs n graph is equal to dτ/dn, since dn is one.  The graph is slightly non-linear; the slope given here is a best-fit straight line, which averages the value of dτ. 

Coin data from the United States Mint

Pendulum Page 1

Pendulum Page 2

Pendulum Page 3

Pendulum Page 4

Coins used in this experiment were taken from circulation: Kennedy half-dollars, Washington quarter-dollars, Roosevelt dimes, Jefferson nickels, Lincoln cents.

 

Coin data taken from US Mint.

 

The coins shown on these pages not used in the experiments. 

 

British pre-decimal pence coins not used.