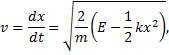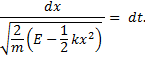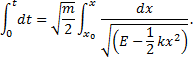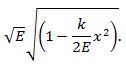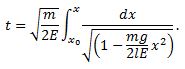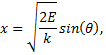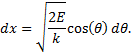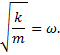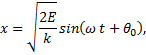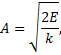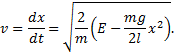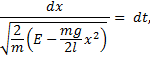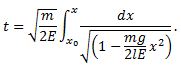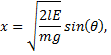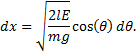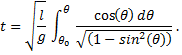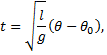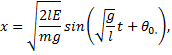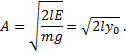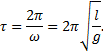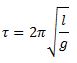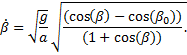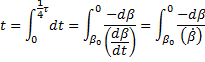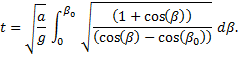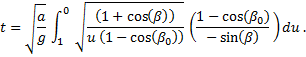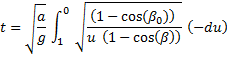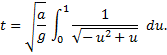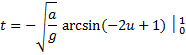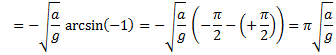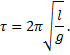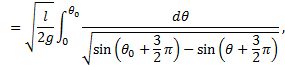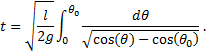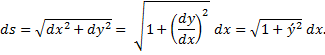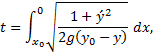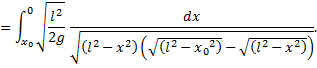PHYSICS HOME

The Pendulum

HOME

Derivation of period equation

 

Newton’s second law

 

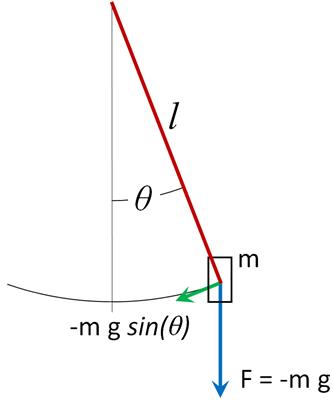
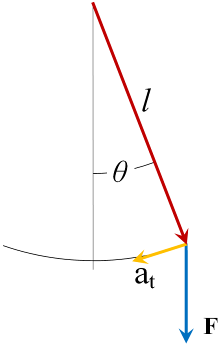
A mass m is suspended at its center by a massless rod of length l and is deflected from equilibrium an  angle θ.  If the top of the rod is attached to a pivot point (ideally frictionless), then under the influence of the force of gravity, F, the mass will oscillate about its equilibrium position.  The force parallel to its motion is

 

where the negative sign indicates the force is directed towards equilibrium.  Let ds be a small distance along the circular arc swept out by the mass, so we have

 

 The time rate-of-change of the position along the arc is the derivative

 

The second derivative gives us the linear, or transverse, acceleration, a_t , of the mass along the direction of its path

 

Applying Newton’s second law to motion parallel to the arc,

 

we have

 

or, rather,

 

Invoking an approximation at this point is in order, so we may find a simple solution to this second order differential equation.  Since the pendulum oscillates over small angles (or, at least, let us resolve to confine the operation of the pendulum to small angles) then we may notice that, under this condition,

 

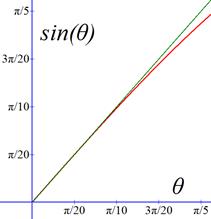
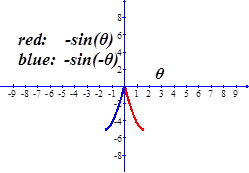
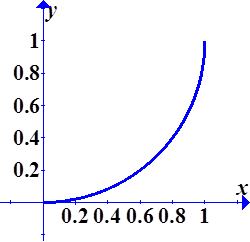
The graph shown below of sin(θ) versus θ, along with a line of slope 45°, illustrates that for angles of a few degrees (certainly less than, say, about 10°) the sine function is very nearly a straight line, thus our approximation is valid.  By the way, the tangent function is also about equal to the sine function for small angles.

 

Sin(θ) in red, straight line in green.

 

 

We now have our differential equation in a more tractable form:

 

which we will solve in a moment.

Potential and Kinetic Energy

 

The equation we derived twice describes the harmonic oscillator, the solution to which has long been established.  We may derive the same equation yet again, this time using energy considerations.  If you imagine a mass, m, undergoing simple harmonic motion by being attached, for example, to a spring (with no other forces in play), then the force on the mass is F_spring = - k x, where k is the spring constant and x is the linear deflection from equilibrium.  The action of the spring is to exert a force on the mass always towards equilibrium, hence the negative sign. 

 

The potential energy, U, residing in the mass while undergoing its harmonic motion is the negative of the work done by the force acting on it as the mass moves from, say, equilibrium to some position x.  We have

 

The kinetic energy of the mass is

 

The total energy, E, of the system is the sum of the potential and kinetic energies.  Because the spring force is conservative, the total energy is constant throughout the motion.  A value for the total energy may be determined by the initial conditions, or perhaps at an extrema of the motion.  For example, if the mass attached to the spring is pulled a certain distance away from equilibrium and let go, then this initial condition at the extreme of the path has determined the total energy; that is, the work done by the pulling force equals the total energy of the system.  Equally, the total energy could be determined if the conditions at any instant are known.  For example, if at some time t the velocity and position are known, then both kinetic and potential energies may be calculated; the energy at that time is equal to the energy at all times.  The total energy is

 

Solve for velocity,

 

and rearrange the differentials:

 

Now write the integral,

 

We could, of course, take some given time t₀ as the time at which our clock starts, but for convenience we have taken t₀ = 0.  We do, however, include the possibility of any starting position, x₀.

 

Remember, we are still considering the mass attached to the spring, not the pendulum, so there are terms for mass and spring constant in the equation.  We are working on a solution to the problem of the harmonic oscillator.  A change-of-variable should make things a bit more simple.  First, notice the x² term; a constant minus an x-squared term brings to mind a certain trigonometric identity [viz., cos²(u) = 1-sin²(u)].  As a step towards this solution, let us rearrange the denominator, thusly:

 

 Integrating the left-hand-side of our equation and substituting in this last expression gives us

 

Now for our change-of-variable; let

 

With this, then, we have

 

And

 

We need now to redefine our limits of the integration.  Let the position x₀ occur at the angle θ₀, and we know then that the position x occurs at an angle θ.  With this, then, our integral, becomes

 

where we have incorporated a more common method of writing the constant in front.  The angular frequency, ω, is defined by

 

Using our trigonometric identity we may finally write, and solve, the integral as

 

We want the solution in terms of x, so we rearrange in terms of θ and substitute:

 

 

The factor that multiplies the sine function, defined as A, is the amplitude of the motion; ω is the angular frequency and θ₀ is the initial phase of the motion.

 

and the relation between angular frequency and period is

 

Back to the question of the pendulum

 

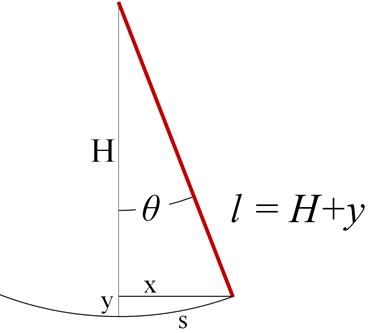
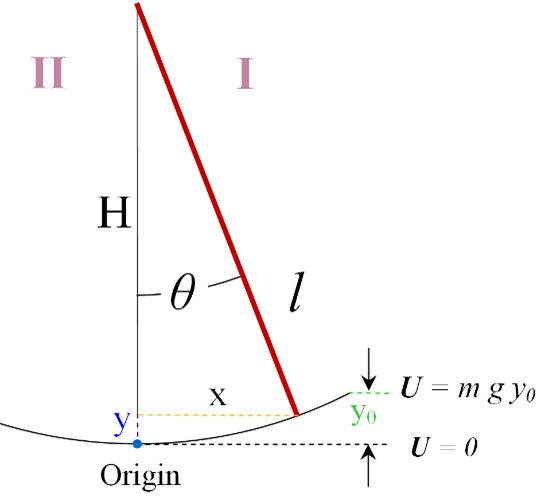
Now getting back to the pendulum, the potential energy of the bob, U, can be written as mgy, where y is the height of the bob above the equilibrium position.  We have previously written the distance along the path as s, and we have made the assumption that the pendulum oscillates over small angles only.  This small angle condition is really the same assumption that the horizontal distance from the bob to the equilibrium position is about equal to the distance along the path, x, as shown in the figure below.  We will write the length of the pendulum as l = H + y; furthermore, we may say that y << l, also a consequence of the same assumption.

 

With these assumptions, then, let’s use the Pythagorean theorem to write

 

 

If, as we say, y<< H, then certainly y² is a lot less than H², and therefore may be neglected.  Also, we invoke the approximate relation H ≈ l, based on the same assumption, of course.  Simplifying the last expression, we now have the approximate relationship we need:

 

which we prefer to write as

 

Now we can write the total energy for the pendulum:

 

Rearrange this for velocity and follow the prescription outlined previously to find the solution.

 

Write the differential as

 

and now the integral,

 

Factor the total energy, E, under the radical as

 

 

Integrating the left-hand-side of equation (D) and substituting in this last expression gives us

 

Now for the change-of-variable: let

 

With this, then, we have

 

And

 

Using the same limits of integration and bringing together all of the factors, we have

 

Using the same the trigonometric identity, we arrive at the solution

 

or,

 

In terms of x:

 

A is the amplitude of the motion for the pendulum and the angular frequency is

 

If y₀ is the maximum height above the equilibrium position to which the bob rises, then the total energy of the system is E = mgy₀ and the amplitude can be written

 

and finally, the relationship we are after, that between period and length:

 

 

Obvious Solution

 

As we wrote above – more than once – the differential equation which describes pendulum motion is

 

It is indeed possible to find a solution much more simply, that is, without recourse to a full mathematical derivation; make a reasonable guess and then see if it is correct.  To begin, notice that this equation includes θ as a function of time, and also its second derivative. These two terms, along with a couple of constants, must add to zero.  We know (from a lot of mathematical experience) that the derivative of a sine function is a cosine, and the derivative of the cosine function returns us to a sine function (albeit negative).  This looks promising as a solution if we can arrange the constants in such a manner that the two sine functions cancel each other by subtraction.  Let us write the general description for a sine function

 

We know to write the function in this manner because we want to include three parameters which describe the sine curve completely.  Here we have A as the amplitude of the sine, some factor ω is the angular frequency – which we will solve for in a moment, and some initial phase, Φ₀. 

The second derivative of our guess is

 

Substituting these two into the differential equation, we have

 

simplifying, we now have ω:

 

The period, τ, of a sine wave is the time to complete one cycle.  Recall that  τ = 2π/ω, so now we write

There we have it.

The Cycloidal-Arc Pendulum

 

If the pendulum bob could be constrained to follow along a cycloidal-arc, then the period is independent of amplitude; furthermore, no small-angle approximation is necessary.

 

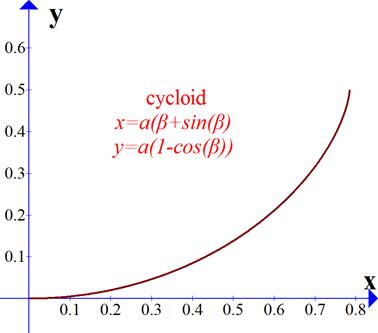
A cycloidal-arc may be written in a parametric representation with the cusp at the origin and open up, as

 

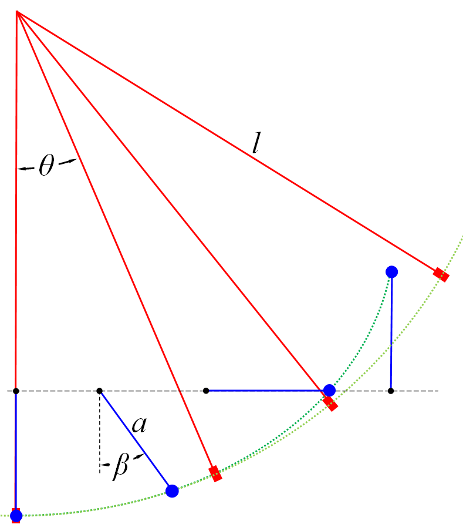
where a is the length of the rotating arm, one end of which also translates along a horizontal line, thus tracing out the cycloid, and β is the rotation angle.  The cycloid is shown in the figure below.  Keep in mind that β is the parameter which describes the cycloidal pendulum angle and is not the same angle as θ, which we have used to describe the circular-arc pendulum; for one thing, their ranges are not identical.  For a quarter-arc, β ranges from zero to π; θ for the circular-arc pendulum ranges from zero to π/2. 

 

The length of cycloid arm, a, is chosen to be 1/4 l in order that period of the cycloidal pendulum be equal to the period of the small-angle circular pendulum (neglecting any circular error, of course).  We shall see this in the mathematics in a moment.  Let the maximum amplitude of the pendulum occur at some angle β = β₀, so the initial height of the pendulum is

 

and the amplitude of the motion is

 

The time it takes for the bob to fall from its initial position to its equilibrium position is one-quarter of the period, τ.  In order to find an expression for this time we write the bob’s kinetic and potential energies, and invoke the principle of conservation of energy.   The kinetic energy, KE, of a bob of mass m is

 

where the velocity of the bob can be written in x- and y-components

 

.

We have, using dot notation for time derivative,

 

 

and

 

so the kinetic energy is

 

The pendulum bob falls under the influence of gravity; we assume no other forces in play.  If the potential energy is defined as zero at equilibrium then the potential energy can be written as a function of the height the bob,

 

The total energy is constant with a conservative force, so we may write the total as the sum of kinetic and potential energies,

 

 

The total energy may be evaluated at any point along the path, so we write the energy at the most convenient point, namely, at the maximum height of the pendulum swing where the kinetic energy is zero and the potential energy is mgy_0.  If we let

 

then

 

or,

 

Solving for the time-rate-of-change of the angle,

 

Now we find the time, t, it takes to fall from some initial angle, β₀, to zero angle.  This is one-quarter of the period, τ/4.  Applying limits, we write the definite integral

 

where we have inserted the differential –dβ  to indicate that the angle is changing in the negative direction.  We now invert the limits in order to remove the negative sign and substitute in for dβ/dt,

 

Variable transformation.

 

We shall use a variable transformation.  Let

 

then,

 

The limits in u are: u = 0 corresponding to β = β₀, and u = 1 corresponding to β = 0.  The integral becomes

 

Inside the radical, place the ratio

 

in order to cancel the sin(β) in the denominator outside the radical.  This leads to

 

Now we use our expression for u to solve for cos(β) and factor the cos(β₀)

 

Now subtract both sides from one,

 

and factor,

 

Substitute this into the integrand and reverse the limits to remove the negative sign, to obtain, finally,

 

We now consult “Tables of Integrals and Other Mathematical Data”, by H. B. Dwight, 4^th ed., MacMillan, 1961, where we find that the solution of an integral of the form,

 

is, under the conditions A < 0 and B² > 4AC,

 

In this case, A = -1, B = 1, and C = 0, so

 

Recall that this is the time for one-quarter of the period, and if we require a = ¼ l, then

 

Thus, the period is independent of β₀.  Furthermore, no small-amplitude assumption has been necessary, so the initial angle may range up to π and the period will have the same value.

 

Comparison of Circular and Cycloidal Pendula.

Intermediate steps in the motion of the two pendula (shown without any coordination between the two angles θ and β).  The cycloid pendulum is shown in blue through a full quarter arc: 0 < β < π; no small-angle approximation is necessary. The circular pendulum, in red, is shown beyond the small-angle approximation.  The period of the circular-arc pendulum has a slight dependence on amplitude, called “circular error”, even with the small-angle approximation.  However, the periods of the two pendula are about equal if a = ¼ l.

 

 

 

 

Circular-Arc Pendulum

 

A pendulum bob undergoing circular motion may be described in a parametric representation as

 

with initial height y₀ at time t₀ = 0,

 

Written in this manner the origin of the coordinate system is at the minimum, and the angle is measured from the equilibrium position.  This

formulation puts the pivot at the co-ordinate ; and the pendulum swings in quadrants I and II.

 

 

The derivatives-with-respect-to-time are:

 

and the kinetic energy is

 

The potential energy is

 

The total energy is constant with a conservative driving force, so at any time, t,

 

where constant may be evaluated at any point along the path, so again we take

 

and

 

Solving for , we have

 

The time it takes for the pendulum bob to fall from its initial position to equilibrium is

 

which, if we use a multiple-angle trigonometric identity, becomes

 

This integral must be solved numerically.  According to Mathematica, the solution is an “elliptic integral of the first kind”. 

Remember, the small-angle approximation is only for the purpose of producing a simple solution to the second-order differential equation describing a simple harmonic oscillator. However, since we are calculating the time for one period (well, four times the quarter-period) we need not restrict ourselves to that small-angle approximation. 

Mathematica code to calculate the period for various initial angles

 

g = 9.80665;

 

L = .993621;

 

“t  calculates the quarter-period.”;

 

"Part I";

 

"enter here an initial angle, called initθdeg, in degrees, then convert to radians; display 10 digits.    Example given here:

 

10 degrees.";

 

"θ₀ (degrees) ="

 

initθdeg = 10. 

 

"θ₀ (radians) ="

 

initθrad = 2.0 initθdeg π/360.

 

"Integrate over the angle from θ₀ to zero angle.";

τ = NIntegrate[ , {x, 0.0, initθrad}];

 

NumberForm[τ,10]"Period ="

 

 

"Part II";

 

"Plot the integrand for that particular initial angle just to see what it looks like";

 

"Plot[ ,{x, 0.0, initθrad}]

 

"Part III";

 

"Vary the initial angle, here called aa, from zero to 10 degrees in .286 degree (.005 radians) steps.  For each step,

 

integrate over the angle to calculate the period.  Make a table.";

 

“Insertion of the number 4 calculates the full-period, tau.”;

 

“Create a table of data.”;

Table[NIntegrate[ , {x, 0, aa}], {aa, .005, .17, .005}]

 

"Graph the data in the table.";

ListPlot[Table[NIntegrate[ , {x, 0, aa}], {aa, .005, .17, .005}], PlotStyle->Directive[PointSize

 

[Medium] , Red]]

 

"List the data, ten digits, in a form suitable for using in any graphing program.  Use 'copy as plain text'";

Column[Table[NIntegrate[ ,{x, 0, aa}], {aa, .005, .17, .005}]];

 

NumberForm[%,10]

 

webpages and Eos image copyright 2016   M  Nealon

Circular Error in Cartesian Coordinates.

 

We may write an expression for a circle in Cartesian coordinates, thusly,

 

where, for a quarter-circle, 0 < x < l.

 

 

 

 

 

 

 

 

 

For the initial position x₀, we have the corresponding initial y-position

 

and the y-derivative,

 

The time it takes the pendulum bob to travel from initial point A to equilibrium point B is

 

where ds is the differential distance along the path and v is the speed of the bob.  This is, again, the quarter-period of the pendulum.  The differential arc-length may be written in terms of dx and dy using the Pythagorean theorem:

 

Once again, to find the velocity, use conservation of energy considerations, setting the sum of kinetic energy of the bob and its potential energy at any point along the path equal to a constant.  We have

 

or, written in terms of the speed,

 

Now we may construct the integral.  Transforming the limits in terms of x-values, we have

 

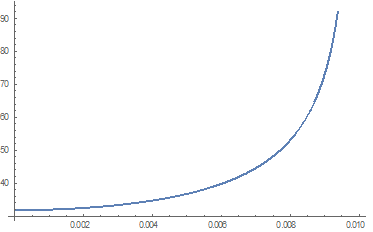
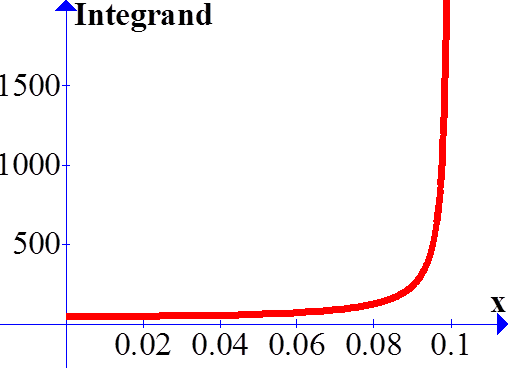
This integral must be solved numerically.  Ordinary graphing software usually has an imbedded “integrate” function which may not be suitable on a plot of this integrand – see below, in red — its difficulty is with the function as it goes to infinity at x₀; so we use Mathematica.

This code in Mathematica,

 

 

 

 

 

 

 

 

 

 

will solve the integral numerically, and produce these results for the quarter-period and plot  the integrand:

 

.5000027003

 

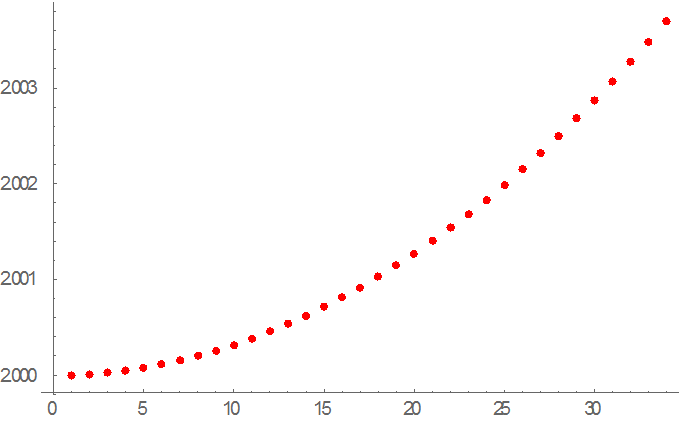
More Mathematica code in Cartesian coordinates, which calculates the circular error for initial amplitudes ranging from .5 cm to 17 cm, in 34 steps (each step is .5 cm).  A 17 cm amplitude corresponds to about 10°.   ListPlot produces a graph as period versus point number (not versus initial angle).  Columns of period and amplitude data suitable for graphing are also printed with this code.

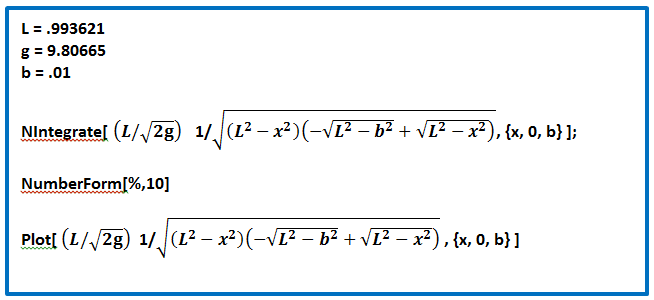
Reference book and links

 

Value for g:                                              http://physics.nist.gov/cgi-bin/cuu/Value?gn|search_for=adopted_in

Regulation rate by coins:                     http://www.parliament.uk/about/living-heritage/building/palace/big-ben/facts-figures/great-clock-facts/

Sound of the great bell:                        http://www.parliament.uk/about/living-heritage/building/palace/big-ben/facts-figures/great-bell/

US coin data:                                           http://www.usmint.gov/about_the_mint/?action=coin_specifications

Cycloid:                                                     http://mathworld.wolfram.com/Cycloid.html

Thermal expansion:                              http://psec.uchicago.edu/thermal_coefficients/cte_metals_05517-90143.pdf

 

D. Lincoln, “Programming and Customizing the PICAXE Microcontroller”, 2^nd edition, Tab Books, 2011. 

Pendulum Page 1

Pendulum Page 2

Pendulum Page 3

Pendulum Page 4

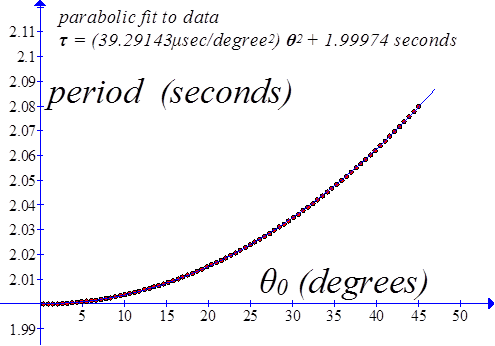
Period as a Function of Initial Angle, Calculated in Mathematica for the Circular Pendulum

Period vs. Initial Angle

Same calculation as above but for greater angles.

Torque and Angular Momentum

 

Another method of deriving this same equation is to consider the angular momentum and torque of the pendulum bob.  Instead of describing the rod as a scalar of length l, we may describe the rod with the vector, , in order to find the torque, , about the pivot point.  Torque is the cross product

 

This torque points along an axis perpindicular to the plane of the pendulum’s motion, and its direction oscillates between positive and negative as the mass swings past equillibrium.  We write the negative of  the magnitude of the torque as

 

We take the negative in order that the maximum torque occur as θ approaches equilibrium.

 

The angular momentum, , of the bob is the cross product

 

which also points perpindicularly to the plane of the motion.  As it turns out, torque is equal to the time-rate-of-change of angular momentum, so we may write

 

The first term on the right-hand-side of this last expression includes which is zero since the length of the rod doesn’t change.  The last term on the right-hand-side incluces which is the linear, or transverse, acceleration, , of the mass.  Note that the mass is not undergoing uniform circular motion since the velocity varies throughout the cycle. 

 

Since the linear acceleration is tangent to the path and thus perpendicular to at all times, we have

 

To write an expression for the acceleration, we recall the differential distance along the path as mentioned above,

 

Since the rod length l is a constant, the velocity is given by

 

and the acceleration, then, is

 

Now substitute this result for a_r into equation (B) and we have

 

Finally, set both equations for torque, (A) and (C), equal; we therefore obtain

 

or, rather,

 

which is the same equation written earlier.

Simple derivation of the differential equation for simple harmonic motion; start with:

F = m a.

Substitute in for a, and substitute in for the spring force:

-kx = m d²x/dt²

or,

0 = d²x/dt² + (k/m) x