
|
EOS |
|
* It is Rocket Science, after all |

|
G Gravity To this point, gravity has been ignored. However, not infrequently are rockets launched in gravitational fields. Close to the surface of a planet, such as Earth for example, the force of gravity may not vary much over a certain altitude so the acceleration due to gravity may be considered as a constant. An object's weight is just the force due to gravity,
where G is the universal gravitational constant = 6.67x10-11 N m2/kg2, gplanet is the acceleration due to gravity near the surface of the planet, Mplanet is the mass of the planet, and y is the distance from the object to the center of the planet.
If the object is on the surface, then y is the radius of the planet, rplanet. Acceleration due to gravity becomes
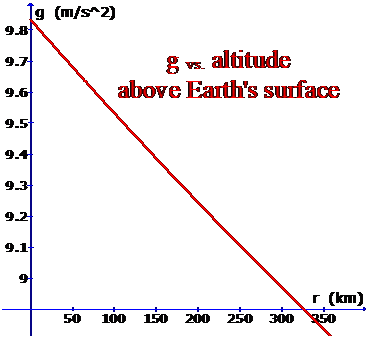
Near the Earth's surface the acceleration due to gravity is about 9.81 m/s2, with slight variations because the Earth is an oblate spheroid of non-uniform density. The radius of Earth is about 4000 miles, so the acceleration due to gravity at a typical parking orbit of a satellite, say, about 200 miles (325 km) above the surface, is less than g at the surface by about 10%. At these altitudes, and lower, we may as well take the acceleration due to gravity to be constant.
To deal with gravity let us return to the rocket equation. The time-rate-of-change of momentum is given by equation (2)
The left-hand side of this equation is the net external force acting on the rocket, previously written as zero without gravity. Including the force of gravity as negative since it is directed in the opposite direction of the rocket motion, the equation becomes
Rearranging,
Considering the equation at some time t puts it in the form to integrate:
This is the same integral as before with the additional term g dt, which becomes
Using results similar as equation (6) for the velocity,
This additional negative term means that the rocket is slowed by the force of gravity. The acceleration is found by taking the derivative of the velocity.
This displacement now becomes
That last term looks familiar.
If the rocket were to move a substantial distance from the planet, the decrease in gravitational force becomes an important factor in the rocket's motion. The acceleration due to Earth's gravity falls to one-half its surface value at an altitude of 1.4 times the radius of Earth. To take this into account, Newton's universal law of gravitational attraction must be used.
where x is measured from the center of the earth, and Mplanet = 5.98x1024 kg, the mass of the earth.
Now the rocket equation becomes:
The position of the rocket, x(t), is a function of time. If you have a solution to this equation, let me know*. |
|
The decrease in g is nearly linear close to the earth’s surface, and falls about 10% at an altitude of 325 km, (200 miles). The altitude of Mount Everest is 8.8 km. The Mesospheric layer of the atmosphere, where meteors burn out, reaches up to about 80 km. The space shuttle orbited at about 200 miles. |


|
The final velocity is the same as in the previous case without gravity except for the negative g tfinal term. This means that the final velocity depends on the duration of the burn and, consequently, a shorter burn results in a greater speed. |

|
Page 1 Momentum Derivation of the Rocket Equation Thrust
Page 2 Speed of the Rocket During the Burn
Page 3 Rocket Acceleration Position as a Function of Time
Page 4 Gravity
Page 5 Saturn V Data Stage 1 Calculation
Page 6 Saturn V Stage 2, Stage 3 Calculations
Page 7 Saturn V Photo Gallery
Page 8 Saturn V Photo Gallery
Page 9 Equation Review |

|
4 Gravity |

|
webpages and Eos image copyright 2020 M Nealon |
|
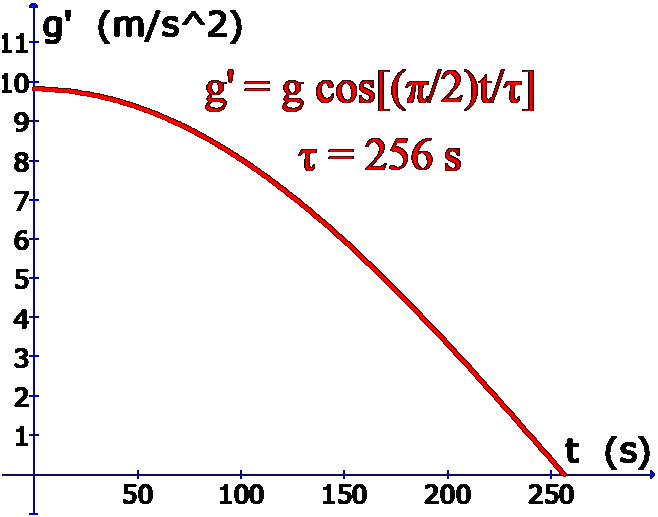
Empirical method of treating the decrease of the component of the force of gravity in the direction of motion as the rocket levels off in its early flight. In this example the rocket lift-off is vertical but is in horizontal motion 256 seconds after lift-off, where g’ = 0. |
|
The rocket motors of the Saturn V are gimbaled, and the trajectory is predetermined by the flight controllers. Although I do not know the exact trajectory, I do know a couple of data points along the path, however. The initial conditions: at t = 0, vr = 0; and, from NASA, we know that at the end of Stage 1, t = 150 seconds and vr = 5330 miles/hour. This is enough information to determine tau. |
|
Air Resistance
The astute reader will have noticed that air resistance has been neglected altogether. The strength of this force acting against the rocket depends on the several factors, most important of which, perhaps, is the speed of the rocket. This drag force may be written as a function linear in speed, but for large, fast rockets, the atmospheric drag may be modeled better by a function which depends on the square of the speed.
Another factor determining the drag force is the density of the atmosphere. For rockets near the Earth’s surface the atmosphere may be considered as having uniform density, but for high flying rockets the density as a function of altitude may have to be included. The atmospheric drag force will depend on the cross-sectional area of the rocket, as well. Finally the force is usually includes a “drag coefficient”. This factor would lump together any other factors, such as the shape of the rocket and the coefficient of friction of the rocket surface. The drag coefficient, written as a number between zero and one, is most likely determined empirically.
Wind may be a more important factor than air resistance. The flight of small rockets might be completely overwhelmed by the wind. For the Saturn V, the exact flight azimuth (compass direction) was determined at launch by considering the wind direction. Launches were scrubbed because of high winds. I will leave it to the reader to investigate the matter of wind on rocket flight.
|
|
For rockets such as the Saturn V – large enough to be put into Earth orbit – a much more significant factor than the decrease in acceleration with altitude is the leveling off of the trajectory just after lift-off. Since the rocket’s motion quickly becomes horizontal, or nearly horizontal, and since the acceleration due to gravity points downward, the component of the force of gravity in the direction of motion is greatly diminished. The component of gravitational force along the direction of motion is given by
where θ is the (pitch) angle between the vertical and the direction of motion. The component of acceleration due to gravity on the rocket, then, is
This angle is a function of time, of course. We could make the simplest assumption that it is directly proportional to time; if so, we might write it as
where τ is a constant which determines the shape of the curve.
|