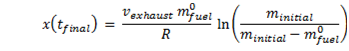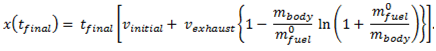Page 3, Rocket Acceleration

Physics Home

EOS

Rocket Science

HOME

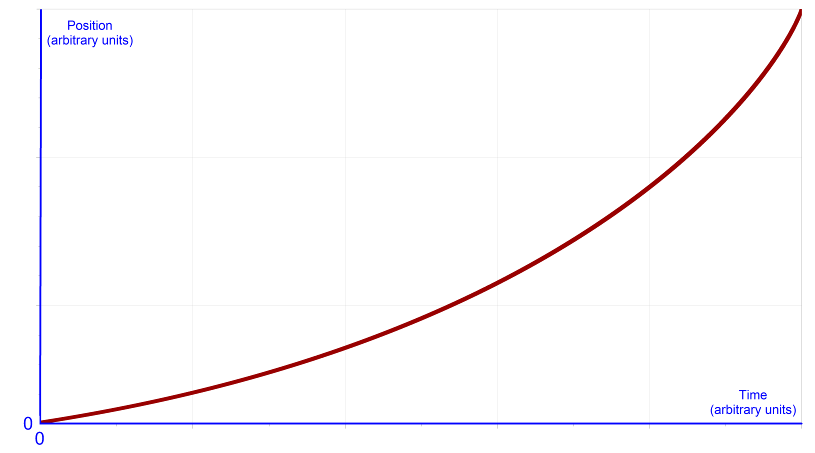
Plot of position vs. time, equation (8), during the fuel burn for a rocket not in a gravitational field and with no atmospheric drag – in other words, in outer space.

* Integrals taken from Tables of Integrals and Other Mathematical Data, Herbert Bristol Dwight, 4^th Ed., MacMillan Pub. Co., 1961

Top

Page 4

Page 2

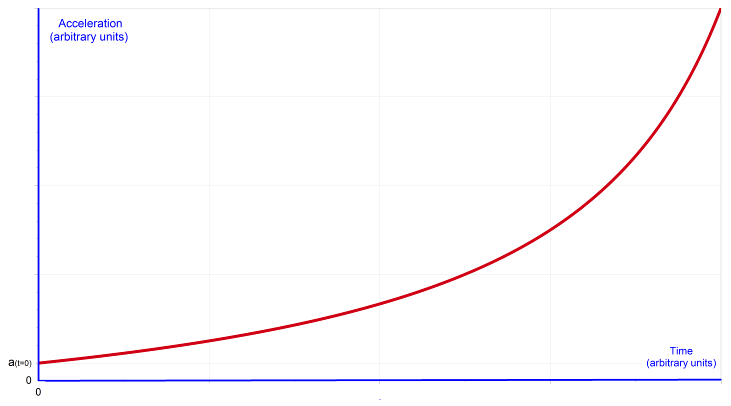
The shape of the a(t) curve for the rocket.

E Acceleration of the rocket.

The engine or motor thrust, T = R v_e_xhaust, is the force acting on the rocket by the expelled gas. The thrust is constant during the burn, but the acceleration is a function of time. Using Newton's second law,

Solving for acceleration,

I will leave it to the reader to show that the derivative of equation (6) with respect to time gives this same result. Note the acceleration at t = 0,

Also notice that the acceleration at the end of the burn is

F Position of the rocket.

We have the velocity and acceleration as a function of time, so we might as well figure the rocket’s trajectory. Well, in one dimension it’s a straight line but I mean the displacement as a function of time.

Start with

The intention here is to integrate equation (6):

Defining the initial condition as x = 0 at t = 0, the position of the rocket at time t is given by

Let’s make a quick substitution so the second integral is a bit easier to handle, namely,

and therefore,

so,

Now put these into the integral. Then

Integrate, re-substitute and evaluate at the endpoints.

Evaluate some of the terms.

Now you can see why I solved for x(t) last!

There’s not much I can do with this last equation, except to notice from equation (4) that u, (the initial mass of the rocket minus the burn rate times t) is just the mass of the rocket at t, namely, m_r(t). [Notice that both equation (7) and the figure showing the burn rate (page 2) give the slope of the fuel mass vs. time as –R.] So, if I wanted to, I could write the position of the rocket as

but I don’t want to. The best thing to do is to plot the thing and see what it looks like.

One thing you might do is to plug in the time which corresponds to the end of the burn to find the rocket's position then (Of course you've noticed already that the equation gives x = 0 at t = 0.). At any rate, recall that