|
Make a quick check to see if we are on the right track. At t = 0 equation (6) is
as it should be; and when the fuel runs out at t = tfinal = m0fuel/R, we have from (5)
Just as we found above in equation (3) for the speed at the end of the burn. |
|
Now, an expression for the rocket mass as a function of time.
Differentiating equation (4) with respect to time gives us
Substitute these last two expressions into equation (2) to obtain an equation which can be integrated.
Integrate the left hand side from the initial speed to some intermediate speed, vr(t), as the right hand side is integrated from t = 0 to some time, t .
Taking the integral and evaluating at the endpoints gives
Substituting in for minitial, we now have the expression
|
|
D Speed of the rocket at some time t. What is the speed of the rocket at some intermediate time during the burn? Consider the mass of the fuel to be a function of time, mfuel(t). Write the mass of the rocket as
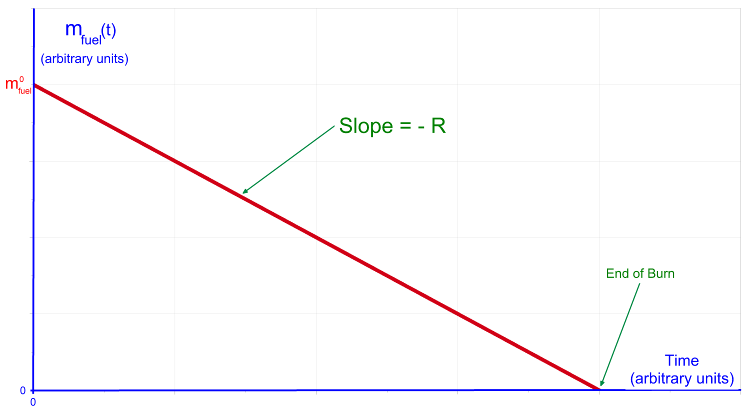
where the mass of the rocket body is still presumed to be a constant. If the fuel burns at the constant rate of – R and the initial amount of fuel is m0fuel, then the amount of fuel at time t is given by
Note that the burn ends at a time
|

|
EOS |
|
Rocket Science |


|
Nowhere in equation (3) is there a variable for the rate of the fuel burn, or, more specifically, the duration of the burn. This means that the final speed is independent of the time it takes for the fuel to burn. Such is not the case if the rocket is in a gravitational field. |


|
* Integrals taken from Tables of Integrals and Other Mathematical Data, Herbert Bristol Dwight, 4th Ed., MacMillan Pub. Co., 1961 |
|
Mass of the fuel as a function of time, burning at a rate R. |

|
C How to figure the speed of the rocket after the burn. Keep in mind that the rocket is accelerating as long as the fuel is burning. Equation (1) above can be written at any time as
where dvr(t) and dmr(t) are differentials. Rearrange this last equation so that all of the mass terms are on one side,
Now it is in a form that can be integrated. Integrate over velocity and mass during the time of the burn. The left hand side is integrated from the initial speed, vinitial, to the speed, vfinal, at the end of the burn; integrate the right hand side from the initial mass, minitial, to the mass at the end of the burn, mfinal.
|
|
Suppose the rocket is in outer space - engine off, with a full load of fuel - and is drifting at a speed vinitial, which may or may not be zero, relative to an outside observer. At this point the total mass of the rocket is minitial. Start the rocket motor and burn all of the fuel. At the end of the burn the rocket has total mass mfinal. The rocket is accelerated to a speed given by
Let’s have another look at the rocket mass. Let the initial mass of the rocket be divided into two parts: the mass of the fuel and all other mass:
where mbody is all of the mass except the fuel, and is a constant, and m0fuel is the mass of the initial full load of fuel.
Since the burn consumes all of the fuel, the final mass of the rocket is just the mass of the body.
With this, we now have
Therefore, the speed of the rocket at the end of the burn is
|
|
Page 1 Momentum Derivation of the Rocket Equation Thrust
Page 2 Speed of the Rocket During the Burn
Page 3 Rocket Acceleration Position as a Function of Time
Page 4 Gravity
Page 5 Saturn V Data Stage 1 Calculation
Page 6 Saturn V Stage 2, Stage 3 Calculations
Page 7 Saturn V Photo Gallery
Page 8 Saturn V Photo Gallery
Page 9 Equation Review |
|
2 Speed |
