Home

EOS

Instruments

Radio Telescope

HOME

Instruments Home

Part A.

How to Set Up the

de l’Est Observatoire Solaire

Radio Telescope

Text Box: I. Level the tripod and orient it to the north compass point as shown in the photo. The top of the blue wedge faces north. Attach the shelf with three U-bolts below the large knurled rating nut. The shelf will hold the Channel Master signal detector.

Text Box: The tripod was manufactured by Criterion for a polar mount telescope (now long gone) with a “U” shaped yoke. The blue wedge is made to be used as shown in this photo so that the center of mass of the telescope is more directly over the apex of the tripod for greater stability.

Text Box: The diameter of the radio telescope Lazy Susan is too large to mount on the tripod in the same manner as the optical telescope so the radio telescope is mounted on the tripod’s blue wedge the wrong way around as shown in the top photo. The blue steel brackets which support the wedge are too long when using the wedge as we are, so the shorter wooden brackets are used along the sides of the wedge to secure it.

Text Box: At times the radio telescope may be used with the blue wedge at zero angle, or “flat”, as shown here. Whenever this is the case you must secure the blue wedge with the wooden brackets. It is just possible, if the radio telescope is set very far forward, for the center of mass to overhang the tripod and cause the blue wedge to lift and fall unexpectedly. This may occur when the telescope is pointed toward the north direction.

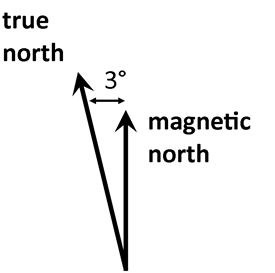
Text Box: II. Attach the Lazy Susan base to the blue wedge. Use four 5/16” x 1” bolts. Before tightening, insert the 5/16” x 2 ¼” clamping bolt (with the 5-star knob) from the underneath side of the blue wedge just to make sure it aligns smoothly with the center hole of the Lazy Susan. [The blue wedge won’t lie in the flat position with this clamping bolt inserted.] Also, use a compass to make sure that the center line of the Lazy Susan base is aligned along the north-south direction. True north is 3° west of magnetic north in Oklahoma.

Tools useful in the assembly of this radio telescope:

7/16” open end wrench 1/2” open end wrench

7/16” socket and ratchet Compass

Small screwdrivers

Text Box: Note: The copper pointer used to indicate the angle at which the radio telescope is aimed may be attached at any time with the two #4 x ½” machine screws. If the blue wedge is in the flat position this angle is the azimuth. The circumference of the top of the Lazy Susan is 36.0” so each tenth of an inch corresponds to one degree.

Text Box: III. Attach the grey base of the radio telescope mount to the top of the Lazy Susan with four 5/16” x ½” bolts - without washers. Use the blue bolts; these are short enough not to interfere with the motion of the Lazy Susan. Before tightening the bolts, again insert the 5-star knob clamping bolt through the bottom of the blue wedge through the Lazy Susan. This time, align it with the nut which is attached to the center of the grey base. Make sure that the bolt turns easily in the nut as you tighten the four blue bolts securing the grey base. Remove the 5-star knob clamping bolt. This clamping bolt can be used later, along with the cork or rubber wedges, to prevent the Lazy Susan from turning.

Text Box: IV. Attach the grey shaft of the radio telescope to the grey base using four ¼” x 1” bolts, star washers and nylon washers. The nylon washers aid in smoothing the motion of the shaft when setting the angle. Place the star washers over the bolt first, then one nylon washer. The two top bolts, but not the two bottom bolts, have a second nylon washer on the inside the flange of the grey base. For the moment, bolt the grey shaft upright, at 90°.

Text Box: V. Attach the grey bracket-with-arm assembly to the top of the 2” diameter grey shaft. Be sure to clamp the assembly securely to the shaft since it is held with only two ¼” x 1” bolts. The arm-assembly is designed to rotate over a range of about 45°. Use eight nylon washers on the four ¼” x 1” bolts, inside and outside the flanges.

Text Box: VI. Pass the white three foot long coax cable with f-type connector through the arm of the grey bracket-with-arm assembly and connect it to the LNB. Attach the LNB to the arm with a single ¼” x 1” bolt and matching nut. The LNB is a loose fit in the arm so clamp it securely.

Text Box: Note: The LNB, low noise block, is the “downconverter” device at the end of the arm which receives the weak microwave signal, amplifies it and converts it to a lower frequency which is more easily transmitted by wire. The first stage amplifier is designed for very low noise. The word “block” refers to a block of frequencies (rather than a single frequency or narrow band of frequencies) which the LNB can receive.

Text Box: How to Import the US Naval Observatory Table into a Spreadsheet How to turn a table from the US Naval Observatory website into usable data for LoggerPro or Graph //////////////////////////////////////////////////////////////////////////////////////////////////////////// From this webpage: http://aa.usno.navy.mil/data/docs/Dur_OneYear.php#notes How to Import the Table into a Spreadsheet Open your favorite text editor, then copy the numerical part of the table (i.e., do not copy the table headings) from your browser and paste it into the text editor. Save the data as a text file. In Excel 2003, click Data on the menu bar, then Import External Data, then Import Data. Select your saved text file. Choose fixed width in the dialog box. [In Excel 2004 for Mac, the commands are Data -> Get External Data -> Import Text File] In Excel 2007, click Data on the menu bar, then From Text. Select your saved text file. Choose fixed width in the dialog box. ///////////////////////////////////////////////////////////////////////////////////////////////////////////// Notes: Favorite text editor = Notepad Which can be found here: Start>>All Programs>>Accessories>>NotePad Save these as text files here: Documents>>Astronomy>>RadioTelescope Then open Excel and follow instructions to import the text file as data. Just keep clicking Next and it should work. Then open LoggerPro, copy the altitude and/or azimuth columns from Excel and paste it/them into a data column. For the x-axis in LoggerPro, open Data>>New Manual Column, then click the Generate Values box; use increment either 1 or 10 minutes as necessary.

Text Box: Short version instructions: 1. Level the tripod and orient it to the north compass point, as described above. Use the bubble level attached to the tripod. 2. Rotate the Lazy Susan so the dish points due south, azimuth 180°. 3. Adjust the blue wedge to latitude 35°. 4. Adjust either, or both, the grey bracket-with-arm assembly and the 2” grey shaft to obtain a chord angle 96.4° with the horizontal, towards the front of the dish. The angle meter will read 180° - 96.4° = 83.6°. The chord will be 6.4 degrees past vertical. 5. Tip the dish forward or backward by the declination angle of the sun on the day of the observation.

North Tripod mount for use with radio telescope.

USNO Sun’s Altitude/Azimuth calculation page:

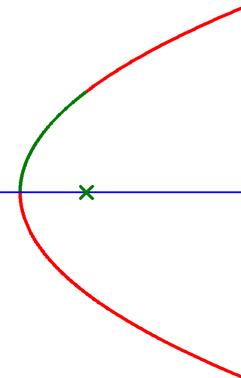
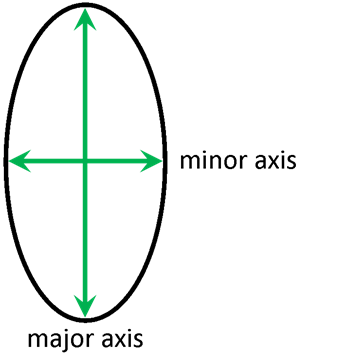
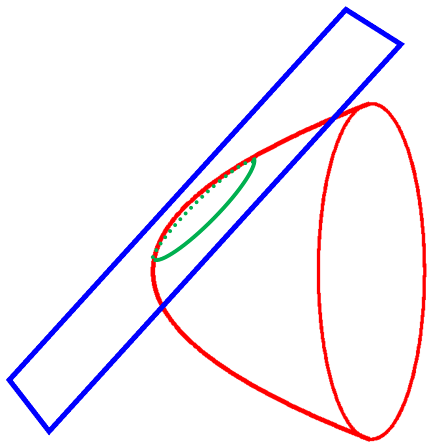
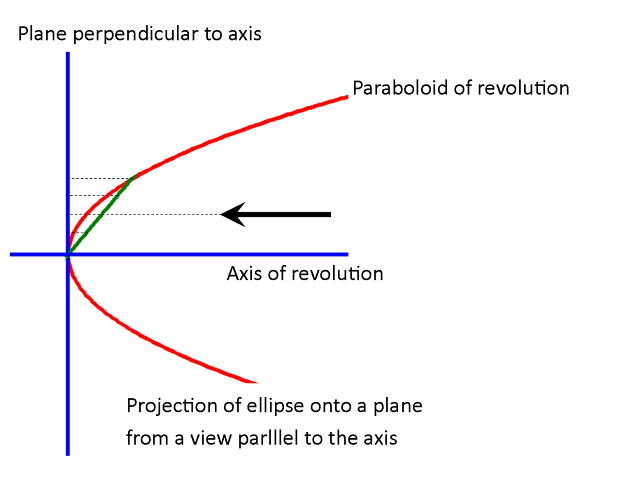
http://aa.usno.navy.mil/data/docs/AltAz.php

Text Box: D. Paraboloid property #1 (or, rather, unproved assertion #1). Consider the intersection between a plane, blue in Figure 6, and a paraboloid of revolution. If the axis of revolution is perpendicular to the plane then the intersection will be a circle. If the axis of revolution is in the plane then the intersection will be a parabola (as shown in cross-section in Figure 1. However, if the plane is obtuse to the axis of revolution, as in Figure 6, then the intersection is an ellipse [property #1]. Thus, the outline of the offset satellite dish is an ellipse. The long way across an ellipse is called the major axis and the short way across is the minor axis as shown in Figure 7. The red chord in Figure 4 is the major axis of the elliptical rim of the satellite dish.

Part B.

How to Aim the

de l’Est Observatoire Solaire

Radio Telescope

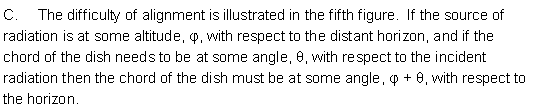
Text Box: C. The difficulty of alignment is illustrated in the fifth figure. If the source of radiation is at some altitude, φ, with respect to the distant horizon, and if the chord of the dish needs to be at some angle, θ, with respect to the incident radiation then the chord of the dish must be at some angle, φ + θ, with respect to the horizon.

Text Box: A. The radio telescope dish is parabolic (strictly speaking, the two-dimensional surface is a paraboloid of revolution) but unlike some common parabolic dishes the focal point is offset. These “offset” type of dishes are obvious if you notice that the receiving elements are usually in line with the edge of the dishes. This first diagram, Figure 1, shows a cross-section of a parabolic dish symmetric about the axis of revolution (blue line). The reflection properties of a parabolic dish are well known. The “x” indicates the location of the focal point, which is “centered” in the dish. The green portion represents the part of the curve which is used as the dish and alone is itself parabolic, of course.

Text Box: B. A satellite dish of the design of the Figure 3 has no physical or mechanical part which is parallel to the axis so it not obvious how to align the dish with the incident radiation, in other words, just which part of the dish points toward the satellite is not necessarily clear. Perhaps the most useful reference line on the offset parabolic surface, shown in Figure 4, is an imaginary chord drawn across the front of the dish from top to bottom as shown in cross-section. The angle, θ, between this chord and the axis will be used for alignment.

Text Box: Figure 2 illustrates more clearly how the focal point is offset. The reflection properties of the offset parabolic curve are the same as in Figure 1. Figure 3 shows the layout of the offset satellite dish, indicating a receiver at the focal point. The arrow indicates the direction of the incident radiation which will be focused at the receiver. This direction is parallel to the axis of the paraboloid of revolution and the satellite dish is “aimed” along this line to receive this signal.

Text Box: F. An inspection of Figure 10 shows how to calculate the angle between the chord and the axis of revolution. The length, D, of the chord across the front of the dish can be measured; it is the major axis of the dish. The height, h, of the dish can be determined easily enough: since the dish appears as a circle the height is equal to the width of the dish. The width of the dish can be measured easily also; it is the minor axis of the ellipse. Thus the angle, θ, can be found from the geometry of triangle D h A in Figure 10.

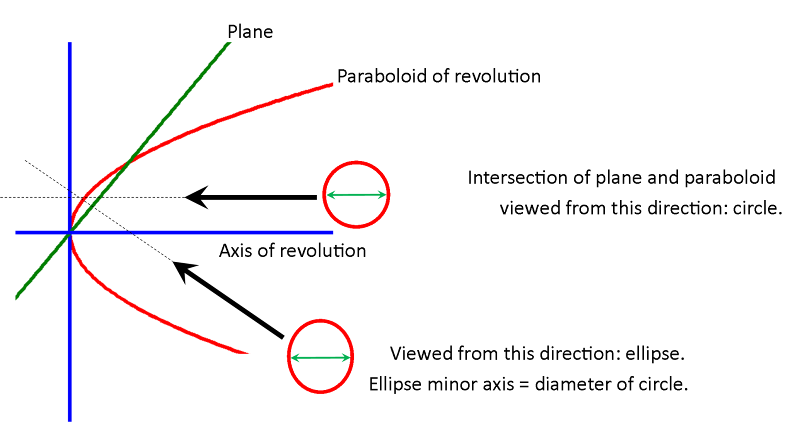
Text Box: E. Paraboloid property #2 (unproved assertion #2). Everyone knows that a circle viewed from an obtuse angle may appear as an ellipse. Perspective drawing on a two-dimensional canvas relies on this illusion. It is also true that an ellipse, looked at from a certain angle, appears as a circle. If Figure 7 is printed onto a piece of paper, then it will appear as a circle if the direction of view is a very low angle just above the paper (look along the direction of either axis). This illusion occurs because the outline appears as though it were projected onto a plane perpendicular to the line of sight. If the elliptical outline of the intersection between an obtuse plane and a paraboloid of revolution is projected onto a plane perpendicular to the axis of rotation, the result is a circle [property #2]. This is illustrated in Figure 8. Figure 9 shows two views of the dish. In one view the dish appears as a circle. The other view is from the direction perpendicular to the chord.

$Text Box: Part II Application To track the sun with the radio telescope (no motor; track by hand): 1. Level the tripod and orient it to the north compass point, as described above. Use the bubble level attached to the tripod. 2. Rotate the Lazy Susan so the dish points due south, azimuth 180°. 3. Remove the lower bolt of the grey bracket-with-arm assembly (at the top of the 2” grey shaft). Adjust the angle so that the 45 degree mark aligns with the center of the nut. 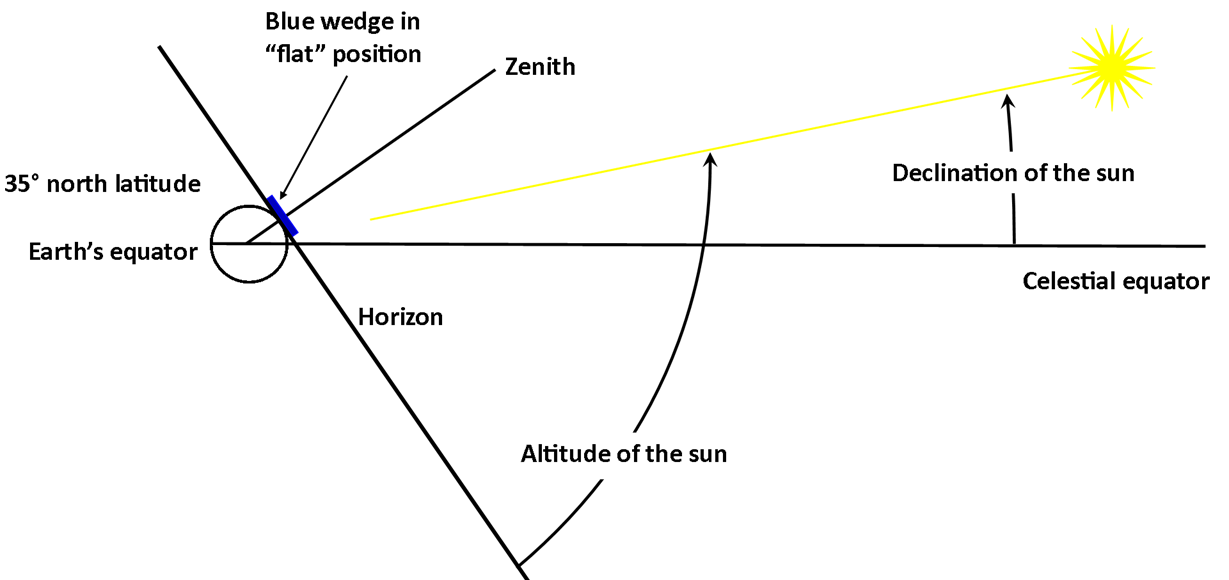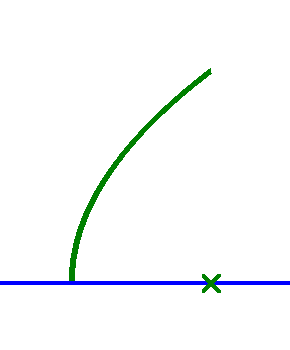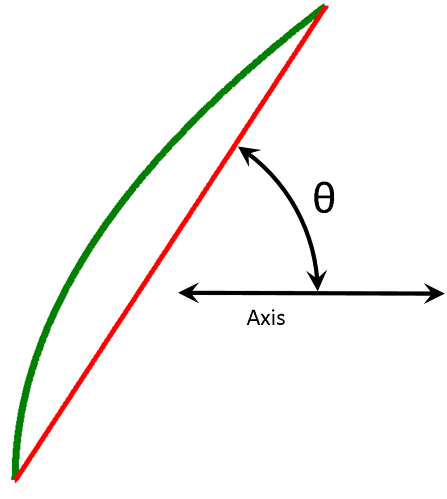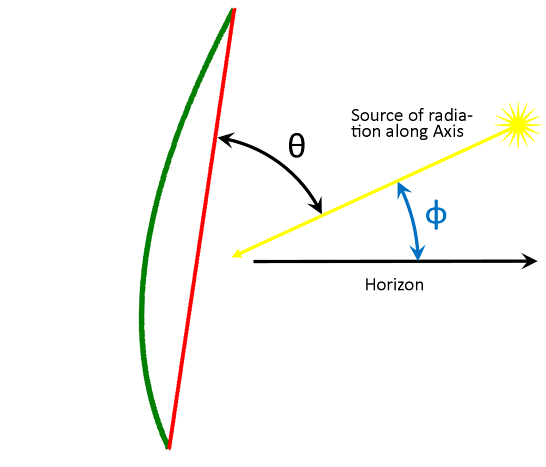4. Use the grey square-steel tube as a cord across the front of the dish from top to bottom as shown in figure 4. Place the digital angle meter on the grey square-steel tube and tip the 2” grey shaft so the chord is at an angle of 61.4° with the horizontal (towards the front of the dish). The angle meter will read 180° - 61.4° = 118.6. The dish is now pointed at the horizon. See figure below. 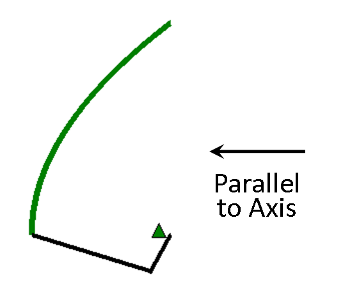5. Place the angle meter along the center line of the Lazy Susan and tip the blue wedge to an angle equal to the latitude. At EOS, that angle is 34.9°. Secure the wedge with the wood brackets. This adjustment makes the tripod a German equatorial mount. See figure. 6. Now the dish is pointed at the celestial equator. The chord across the front of the dish will be at an angle of 61.4° + 34.9° = 96.3° with respect to the horizontal (towards the front of the dish), although the angle meter will read 180° - 96.4° = 83.6°. The chord will be 6.4 degrees past vertical. 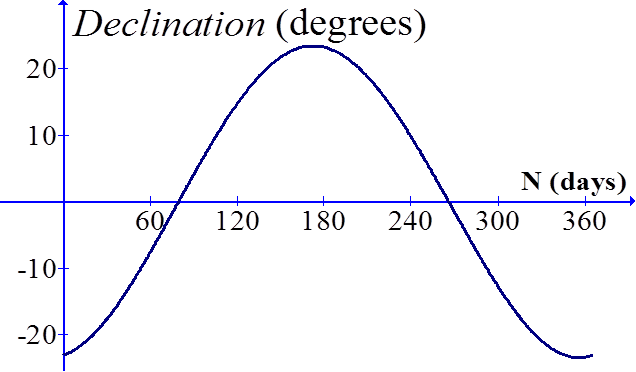7. In order to aim the radio telescope at the sun, now rotate the grey bracket-with-arm assembly (either up or down) to an angle equal to the sun’s declination on the day of the observation. The range of declination values over the course of one year is ± 23.44° . The dish may now track the sun if the Lazy Susan is rotated. To keep the dish from turning inadvertently, use the five-star knob, and/or place the rubber and cork wedges under the Lazy Susan. Find the declination. The declination of the sun may be found in a number of ways. A. Use the calculator found at the NOAA website. http://www.esrl.noaa.gov/gmd/grad/solcalc/ Or try this old version. To use this version the latutide and longitude of the dish location are required. http://www.esrl.noaa.gov/gmd/grad/solcalc/azel.html B. Use a good planetarium program such as Starry Night. To use that particular program, first make sure that the time is set to the correct day. 1. Place the cursor on the sun. If the cursor is properly on the sun, information about the sun will appear in the upper left corner of the screen. Now, right-click on the sun, then left-click on “Select Sun”. 2. Now left-click on the “Info” tab along the left side of the screen; a box will open. The top line of the box should read “Name: Sun”. Scroll down to the box “Position in the Sky” and read the entry: Dec (JNow) C. Calculate the declination using an approximate equaton, such as this one: δ ≈ -arcsin[0.39779*cos(0.98565*{N+10}+1.914*sin(0.98565*{N-2}))] where N is the number of days from midnight UTC, January 1, to the day of the observation. Integer days should be accurate to within the ability to adjust the dish angle; however, fractional days will give greater accuracy in the declination. Be sure your calculator or math software is working in degrees, not radians.$

Step 3. Remove the lower bolt. Adjust the angle so that the 45° mark aligns with the center of the nut.

N = day of the year = cumulative days + day of the month

January N = day of the month

February N = 31 + day of the month

March N = 59 + day of the month (for non-leap year)

April N = 90 + day of the month

May N = 120 + day of the month

June N = 151 + day of the month

July N = 181 + day of the month

August N = 212 + day of the month

September N = 243 + day of the month

October N = 273 + day of the month

November N = 304 + day of the month

December N = 334 + day of the month

For leap years, 2016, etc., add one to the cumulative days for March or later months)

Fig. 1

Fig. 2

Fig. 3

Fig. 4

Fig. 5

Fig. 7

Fig. 6

Fig. 8

Fig. 9

Fig. 10

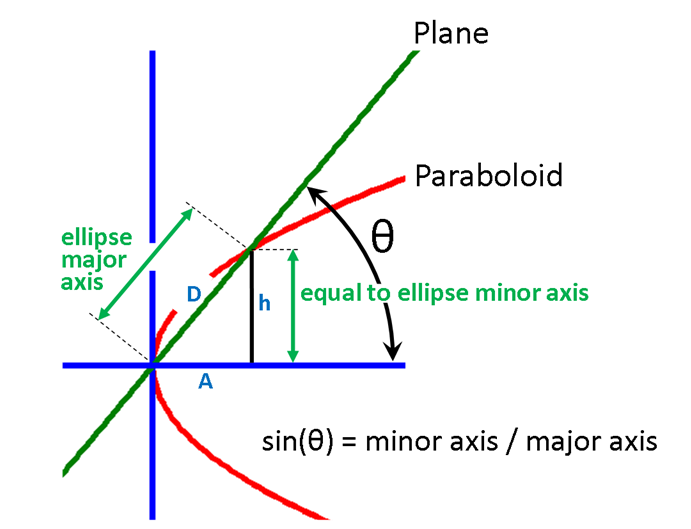
sin (θ) = h/D,

or,

θ = arcsin(h/D) = arcsin(minor axis/major axis).

Step 4. Blue wedge in flat position and dish is aimed at the horizon.

Step 5. Blue wedge adjusted to an angle equal to the latitude. Dish is now aimed at the celestial equator.

The next step, 7: To aim the dish at the sun, tip the dish an angle equal to the sun’s declination.

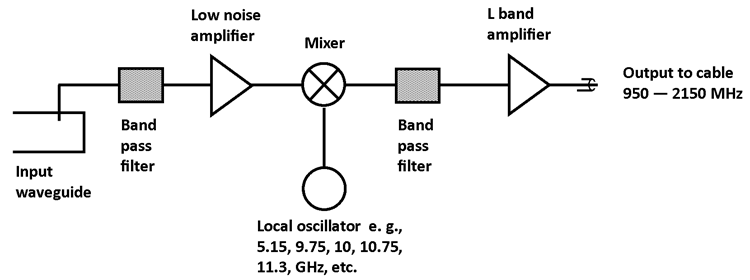
Input frequency band from satellite waveguide	Input band GHz	Local Oscillator (LO) frequency GHz	Output L band into cable MHz	Comments
C band	3.4-4.2	5.15	950-1750	inverted output spectrum
	3.625-4.2	5.15	950-1525	"
	4.5-4.8	5.75	950-1250	"
	4.5-4.8	5.95	1150-1450	"

Ku band	10.7-11.7	9.75	950-1950
	10.95-11.7	10	950-1700
	10.95 - 12.15	10	950-2150	Invacom SPV-50SM
	11.45-11.95	10.5	950-1450
	11.2-11.7	10.25	950-1450
	11.7-12.75	10.75	950-2000	Invacom SPV-60SM
*	12.25-12.75	11.3	950-1450	Invacom SPV-70SM
	11.7-12.75	10.6	1100-2150

Ka band	19.2-19.7	18.25	950-1450
	19.7-20.2	18.75	950-1450
	20.2-20.7	19.25	950-1450
	20.7-21.2	19.75	950-1450
	19.7-20.2	21.2	1000-1500	Inverted
	18.2-19.2	17.25	950-1950	Norsat 9000
	19.2-20.2	18.28	950-1950	Norsat 9000
	20.2-21.2	19.25	950-1950	Norsat 9000

nominal 18” grey DishTV brand satellite dish

Minor axis = 18.0”

= 457.2 mm

Major axis = 20.5”

= 520.7 mm

θ = 61.4°