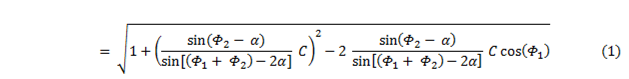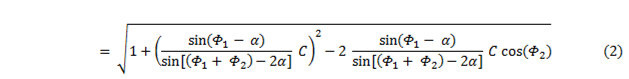EOS

Astronomy

 

5

HOME

Astronomy Home

Kepler’s war with Mars

Kepler’s War with Mars

Page 1

Page 4

             Here is some data* taken by Tycho Brahe, published in “Basic Astronomy Labs” by Huebner, et. al.  (Although Brahe’s original data is available, this author has not been able to confirm the provenance of this particular data set.)  Notice that the data come in pairs – each pair corresponds to two observations of Mars taken one Martian year apart.  The data are given not in terms of elongation but rather in terms of the geocentric (earth-centered) longitude, Ω, of Mars.  This angle is measured in reference to an axis parallel to the same axis used to measure the heliocentric longitude of Earth, the position of earth on the vernal equinox.

             To use this data, first plot the position of earth using the heliocentric longitude.  Mars was observed from earth at that point; to find the line of sight of Mars, set the origin of the protractor on that position of earth and align the axis of the protractor parallel to the line of the vernal equinox.  Mark this geocentric longitude angle of Mars and draw a line from the earth to the mark.  Mars was on this line of sight on that date, but the distance to Mars is unknown.  Do the same with the second data point.  The point where these lines cross was the location of Mars. 

             Oddly enough, these particular five points on the orbit of Mars are sufficient to find the eccentricity of Mars’ orbit.

The Brahe Campaign

*Basic Astronomy Labs, Huebner, Reynolds, Smith, Prentice Hall, 1996

             Plot Brahe’s data and you will find five points marking the orbit of Mars.  Three of the points fall close together.  I have plotted the first point for you.  Use a computer graphing program and you can fit an ellipse to find the eccentricity.

             If plotting by hand there really is not enough data to fit easily an ellipse, but the eccentricity can be found none-the-less.  First, draw by free-hand a smooth “best fit” curve through those three points which are close together.  This interpolated curve indicates part of Mars’ orbit.  To find the eccentricity, now try to identify as best you can Mars’ perihelion (nearest approach to the sun [and, by the way, earth’s orbit]) and aphelion (furthest approach).  The perihelion and aphelion will not necessarily coincide with any of the data points.  You may have to extrapolate part of Mars’ orbit from a single data point.  You might approximate a very small part of Mars’ orbit as a short circular arc (with the center point unknown).  Draw a straight line between the perihelion and aphelion of Mars’ orbit.  This line must pass through the sun; this is the major axis.   Bisect the major axis to find the midway point.  This point is the center of Mars’ elliptical orbit.

             Measure (in any convenient unit) the distance along the line you just drew, from presumed perihelion to aphelion and divide that by 2 to find the semi-major axis, a.  Measure the distance, c, from the center of the ellipse to the center of the sun using the same units.  The eccentricity, then, is the quotient

 c/a

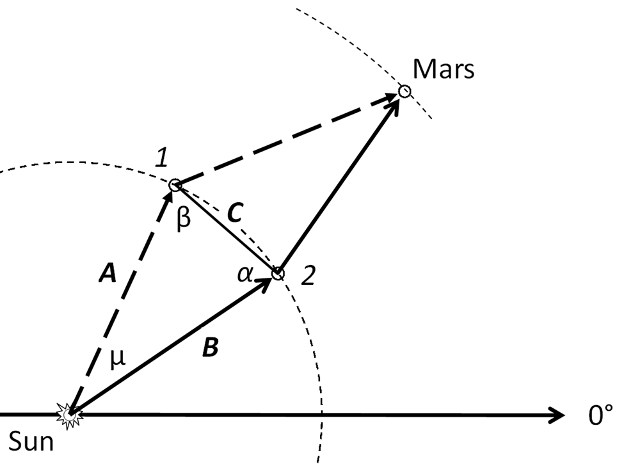
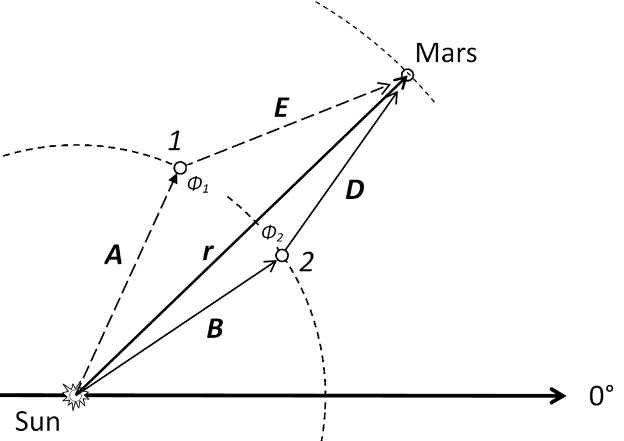
             Consider the triangle ABC, defined by two locations on earth’s orbit.  Enough information is known that distance C can be found.  C is the linear distance between the two locations of earth when the observations of Mars are made.

             The eccentricity of earth’s orbit is 0.01671123, small enough for the purpose of this calculation to consider the orbit approximately a circle.  Earth is at position 1 at some time and then 1.8807 years later is at position 2, so the angle μ is

             The radius of earth’s orbit is used as the unit of distance, the astronomical unit, AU.  So the distances A and B equal 1AU.  The simplest method of finding the length C is to use the law of cosines

             We might as well write the angles α and β while we are at it.  Triangle ABC has two equal sides and is therefore isosceles; this means that the two angles α and β are equal.

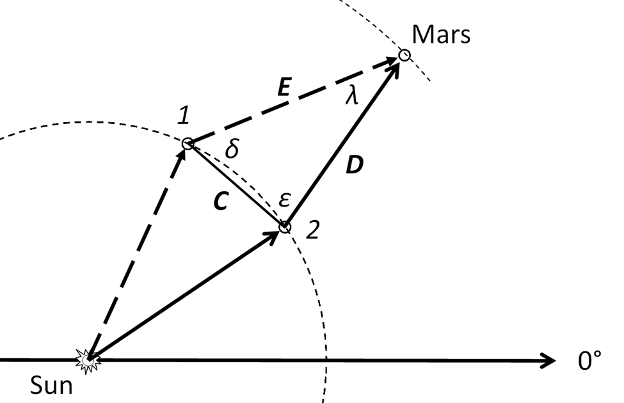
                 Now consider the triangle DEC.  The goal here is to find the distances to Mars from earth, D and E, on the days of the observations.   The angles δ and ε can be determined by subtraction from the elongations.  This is an intermediate step in finding the distance to Mars from the sun.

So the angle λ must be:

Using the law of sines,

the distances E and D can be found,

In order to simplify, we note that

and, since α = β, we have

Furthermore, we can write

and, since sin(180° - ω) = sin (ω)

Now rewrite the expressions for E and D in terms of the observed Φ₁,  and Φ₂.

                 The distance, r, from the sun to Mars is calculated either by triangle AEr or BDr using the law of cosines and the elongation angles.  We have

 

 

or,

 

where

             C = 0.73216 AU, and

                 α = 68.526°.

Kepler’s Battle Plan: Trigonometry

Calculation of the distance from the sun to Mars using the elongation of the first six points along the orbit from the table of planetarium data on page 2.  Either expression (1 or 2) for r may be used.

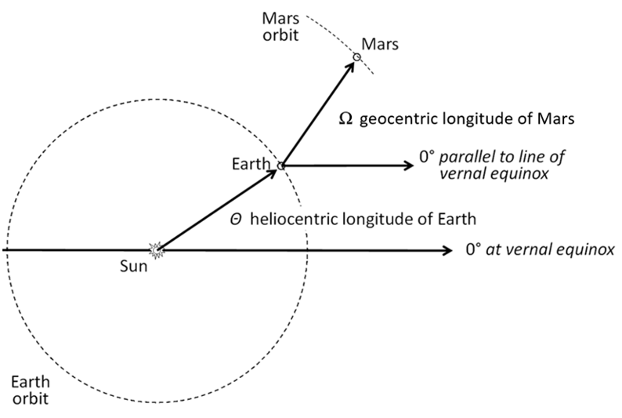
Figure showing the zero degree reference axis for measuring the geocentric longitude of Mars.  The axis remains parallel to the line of the vernal equinox regardless of the location of Earth in its orbit.

 

If required, the angles of geocentric longitude of Mars may be transformed into elongation angles using the heliocentric longitude of Earth.  In this diagram,

 

elongation = (180° - Ω) + Θ.

 

I’ll leave it to the reader to write the transformation for the other quadrants.

Page 1

Keplers Elliptical Orbit .

 

 

Page 2

Orbit Data.

 

 

Page 3

Mars Fact Sheet.  (nasa)

Fear and Panic.

 

 

Page 4

Mars Exploration.

(nasa)

 

 

Page 5

The Brahe Campaign.

Kepler’s Battle Plan.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Photos: nasa

 

All links and photo references valid at time of writing and  in future  will likely never be checked to see if they are still valid.

Exercise for the reader.

 

If the data on the top of this page really are from Tycho Brahe then Kepler is likely to have used it.

It should be possible then to find the distances to Mars which Kepler must have calculated. 

Convert the geocentric longitudes to elongation and use equations 1 or 2 to find the distance.  Two elongations are given.

fin