The Nealon Equation

y  =  (A*sin(B*x+C) + D*sin(E*x+F) + G*sin(H*x+I) + J*sin(K*x+L)) *

 (M + N*x + O*x^2 + P*x^3 + Q*x^4) * atan(R*x) * atan(S*(BL-x))

HOME

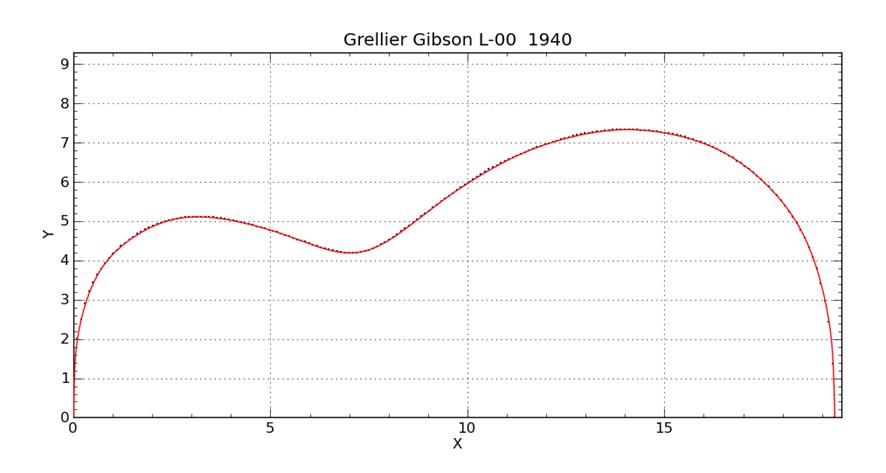
Grellier Gibson L - 00  1940

http://grellier.fr/plans.php?lang=fr

 

 

                                                             “Il manque juste le dessin du truss-rod.”

                                                                                           -  Monsieur Grellier

 

                                                              “J’ai terrassé les dragon.”

                                                                                           -  M  Nealon

(A*sin(B*x+C) + D*sin(E*x+F) + G*sin(H*x+I) + J*sin(K*x+L) + M*sin(N*x+O) +P*sin(Q*x+R) +AA*sin(BB*x+CC))*

(S + T*x + U*x^2 + V*x^3 + W*x^4) * atan(Y*x) * atan(Z*(19.324-x))

  

    A = -4.870808371497193E+02

    B = -7.040688233980210E-01

    C = 4.120054533938742E+00

    D = -4.306401301536174E+02

    E = 4.977584629453556E-01

    F = -4.580063958661442E+00

    G = 1.139460743838969E+02

    H = -3.629481318224734E-01

    I = 5.967975949921605E+00

    J = -2.931127947916925E+02

    K = 7.910758005121563E-01

    L = 1.073424492625578E+00

    M = 5.936152674811037E+02

    N = 5.828210191651341E-01

    O = 6.864819467929281E+00

    P = 6.659725076181603E+01

    Q = 8.798978774860676E-01

    R = 1.324604536132214E-03

    AA = -3.062480293785913E-02

    BB = 2.244453482002917E+00

    CC = -8.624304510787958E+00

    S = 6.947610996856965E-02

    T = -2.515897740961353E-02

    U = 1.718899684067937E-02

    V = -1.937105082084855E-03

    W = 6.223972835296340E-05

    Y = 4.677375788356206E+01

    Z = 3.321710132644738E+01

Coefficients for the Grellier Gibson L-00  1940 guitar

28 Coefficients

This is the best fit I have gotten of all the instruments so far.  Chi squared = .008231

This is getting a little bit out of hand, but I had to use 28 coefficients to obtain such a fit.  Well, at least with modern graphing programs the coefficients can be entered easily - having so many doesn’t make any more work.  I believe that such good fits are required for machining precise body molds and patterns.

 

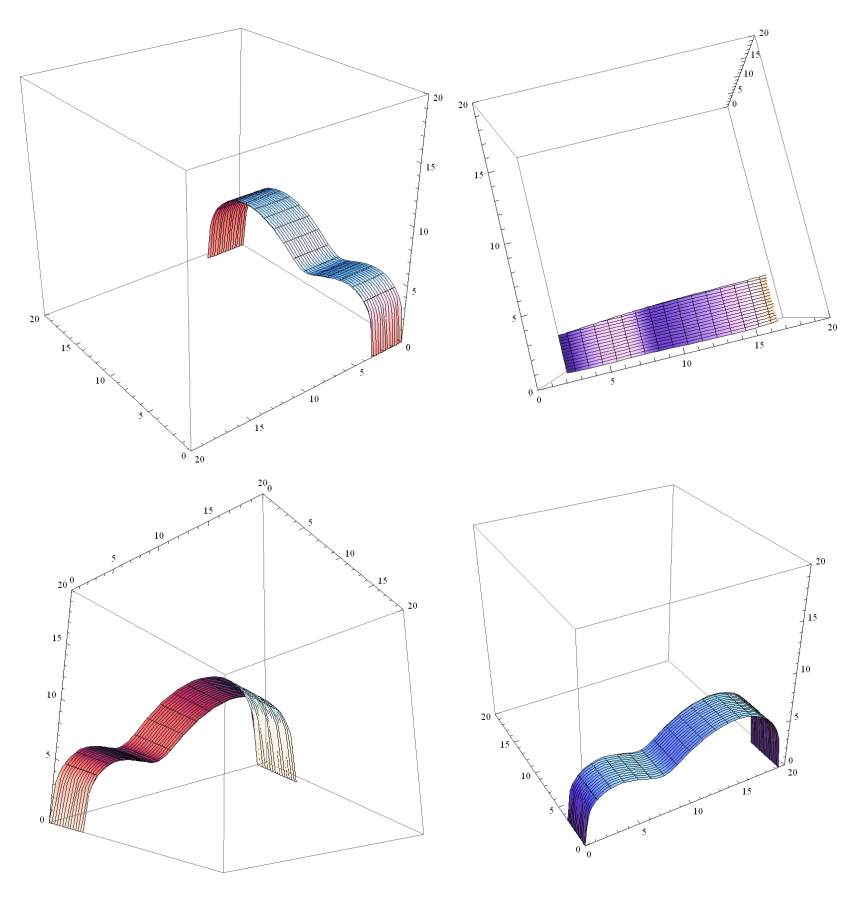
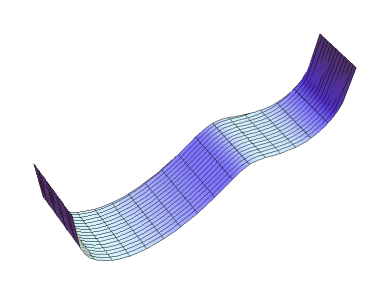
View of the side in Mathematica.

 

 

 

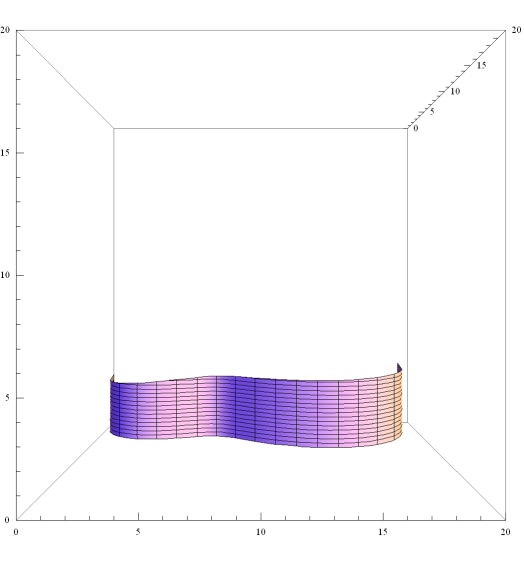
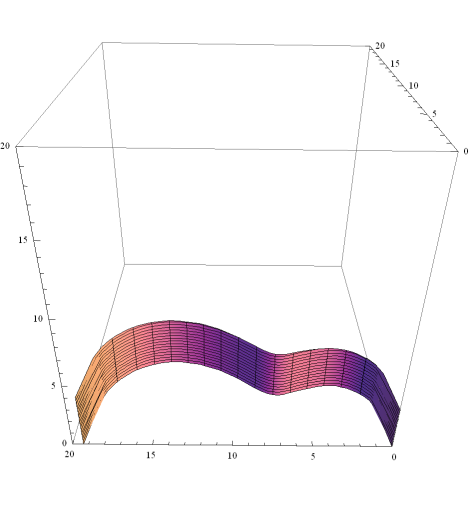
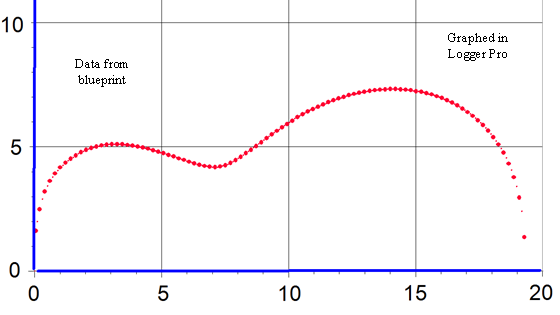
Graphed in Curve Expert Pro

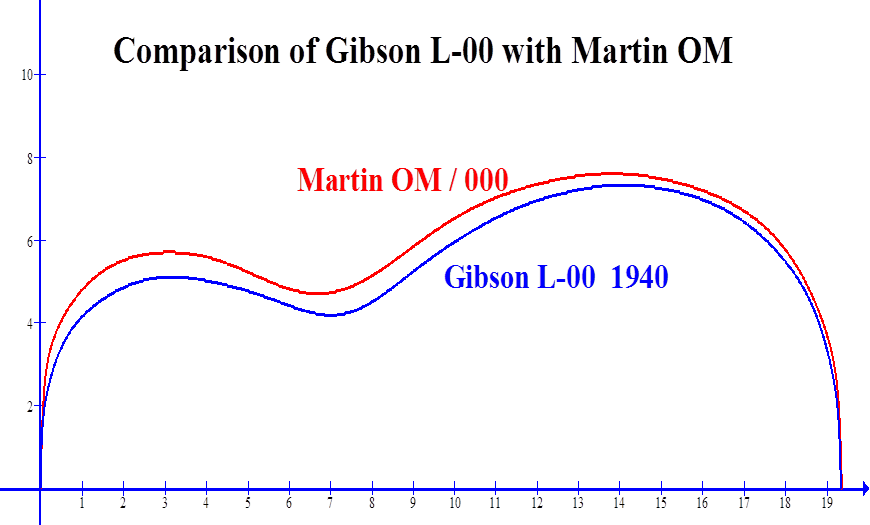
Grellier’s Gibson L - 00  1940

 

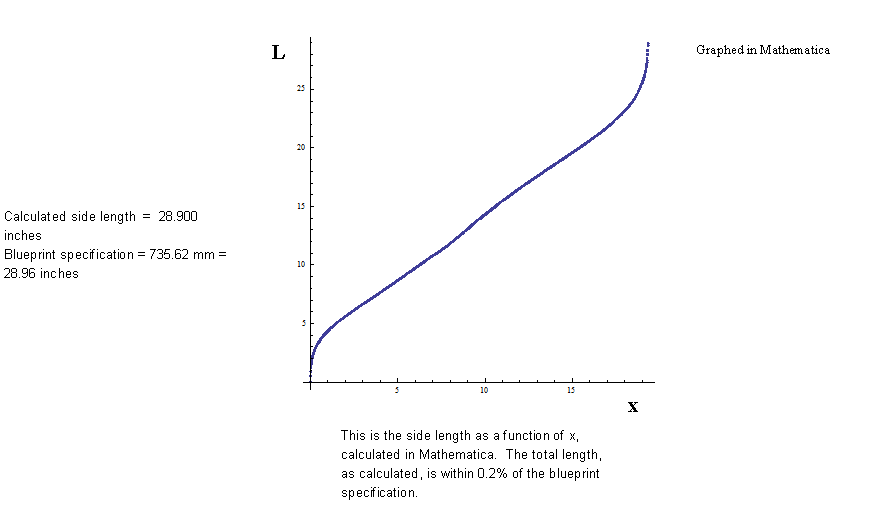
Equation Home Page