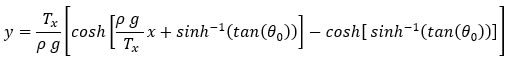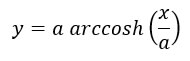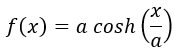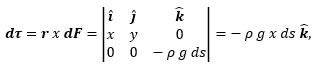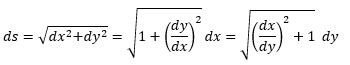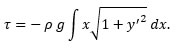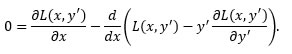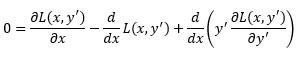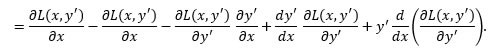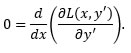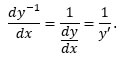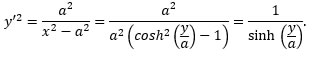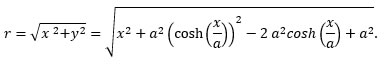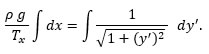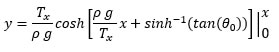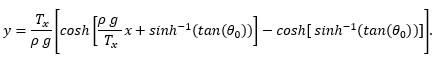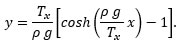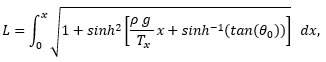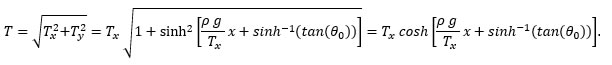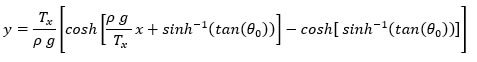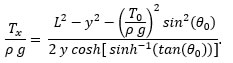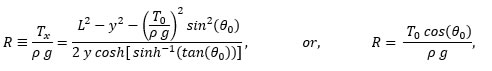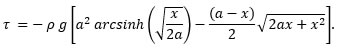
|
A slack rope secured at both ends hangs under its own weight. We consider a differential line segment of length ds, anywhere along the rope. The weight of the rope below the differential line segment adds to the tension acting on the segment, and thus, unlike the horizontal rope, the tension is not constant throughout the length of the rope. |
|
Kite String Theory |
|
Our interest is in the flight characteristics of a kite, and we need to know the mathematical curve which describes the shape of the string while the kite is flying. We derive this curve in two ways: 1) we consider the torque, yes, torque, acting on a string and 2) we consider the tension in the string. Our string is idealized as a flexible one-dimensional material of uniform linear mass density which does not stretch or compress under tension. Our string must be hanging smoothly in a uniform gravitational field under its own weight. The curve we derive, the well-understood catenary, will describe any rope, thread, wire, chain, cable, string, etc., with said characteristics. The kite acts to secure one end of the string. The kite flyer secures the other.
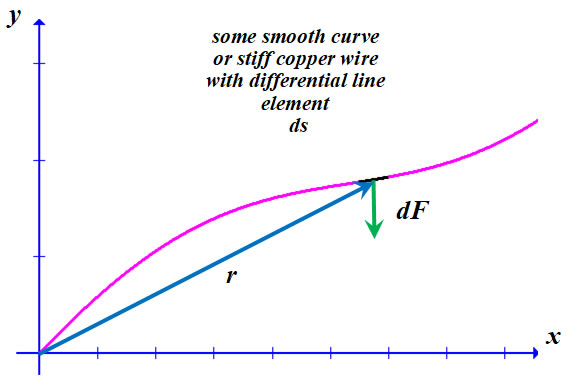
We start with a differential line segment of the string beginning at point A and following some smooth curve to another point, B, as shown in the figure below. The string tension acting on the endpoints of the segment are vectors which are tangent to the curve at their respective points. The vectors are not co-linear since the kite string is curved. The magnitude of the tension at B is greater than the magnitude of the tension at A. |
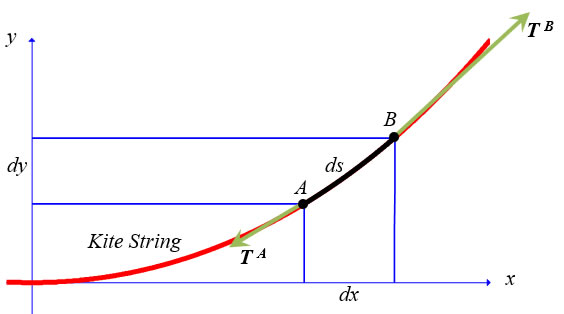
|
Even in the case that ds is of finite length, the horizontal components of the tension vectors at A and B are equal. Let ρ be the linear mass density of the string. The differential mass of the string element, then, is dm = ρ ds and the magnitude of the force due to gravity is dF = dm g = ρ g ds, where g is the (constant) acceleration due to gravity near the earth’s surface.
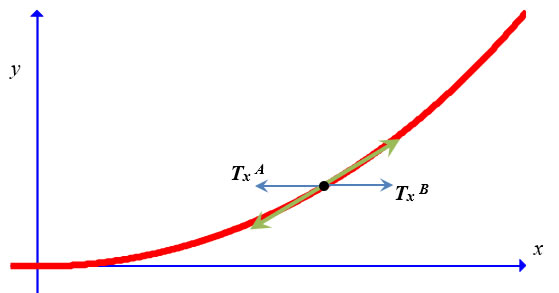
For ds ≠ 0, there is no change in the tension at point A. Since the force of gravity points downward, the change in tension at B occurs only in the y-direction, leaving the x-component unchanged. Thus, the horizontal forces are still equal but opposite, despite that points A and B are not coincident. This last condition is independent of the length of the line segment ds, which means that the horizontal component of the tension is everywhere the same. |
|
Let us look at the horizontal components of the tenson vectors; we aim to show that the horizontal components are equal in magnitude. In the limit as ds → 0 (as B → A for example) we see that the vector TB → -TA since B now coincides with A. Because the string is hanging still, i. e., there is no acceleration of the string, the net force on the string in the x-direction is zero. This means that the horizontal components of the two tension vectors point in opposite directions but are of equal magnitude. |
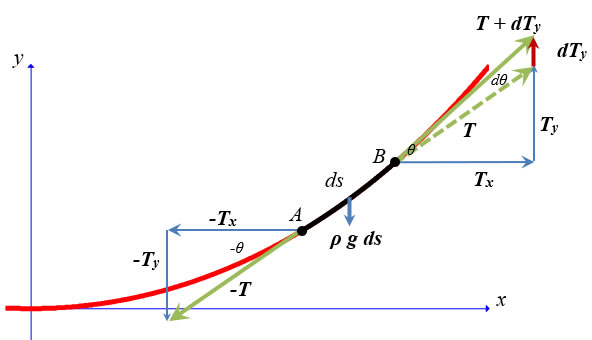
|
Since ds is small, we drop the A and B superscripts and write differential expressions for the tension and the tangent angle. Write the tension vector as -T at point A, and the net tension at point B as T + dTy. See the figure, above, where we show that vector dTy is in the y-direction. If -T at point A makes an angle -θ with respect to the -x-axis, then we may write the tension at point B as the vector T + dTy at an angle θ + dθ with respect to the +x-axis. |
|
Catenary Kite |

|
EOS |

|
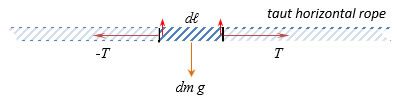
If an unstretchable rope is anchored at one end to an “immovable” object such as a wall, and then pulled taut so that the rope describes a straight, exactly horizontal line, then the pulling force, called tension, is carried by the rope to the wall and the rope pulls the wall with the same tension. The rope is static and the tension is constant throughout the length of the rope. A differential segment of the rope of length, dℓ, has a mass, dm, on which the force of gravity acts vertically downward. Because the rope is not accelerated downward, there must be molecular forces in the material acting upward on the line segment, making the net vertical force zero. The tensional force, T, acts on both ends of the differential line segment. |

|
Physics |
|
Now we return our attention to the tension in the kite string. Writing Newton’s second law with zero acceleration in the y-direction,
or,
Consider now the tangent of the angle,
Solve for the y-component of the tension:
Now, let us take the derivative with respect to x of both sides, recalling that Tx is a constant,
We may rewrite this as
Now make the substitution for dTy
|
|
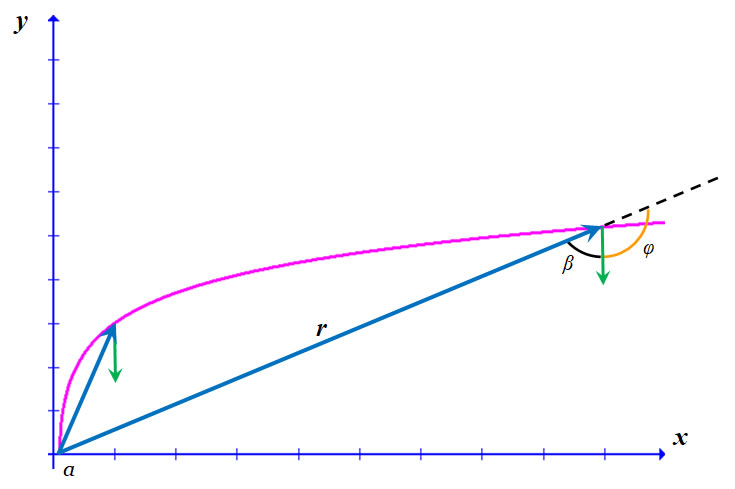
Our kite string follows some as-yet-to-be-determined smooth mathematical curve with end points (x1, y1) and (x2, y2), where we require x2 ≠ x1 and y2 > y1. That is, the string shall not follow a vertical straight line. The earth’s gravitational force exerts a torque on the string. Even though the string is flexible and the string would fall straight down rather than rotate about a fixed axis if separated from the kite, nevertheless, we can calculate the static torque, τ, acting on the string. Since the kite flyer supports one end of the string and the kite supports the other, there is no angular acceleration of the string (for a stationary flying kite). If we like, we could imagine a thin rod such as a stiff copper wire which can be bent into any shape and retain that shape — no kite necessary — as a physical manifestation of our mathematical curve. Further, we would imagine the rod supported at the lower end only, with a clamped hinge. The gravitational force exerts a torque on the rod and the clamp must act against that torque in such a manner that the hinge not turn. Loosen the clamp and the rod rotates with an angular acceleration. We pick a rotational axis parallel to the z-axis, perhaps through the point (x1, y1). Let r represent the position vector from this rotation axis to the line element ds along the string; we also have the vector differential force dF due to gravity acting on the string. Then,
and
which points in the – y-direction. The differential torque is the cross product
and the magnitude of the total torque can be found by the line integral
The differential element of length
can be written in terms or either dx or dy,
where we use the prime notation to indicate the derivative. The same result obtains whether we integrate along the x- or the y-axis; we chose the dx form. The integral gives us the magnitude of the torque
The torque vector is
which points in the – z-direction. |
|
Variations on a String |
|
We cannot perform this integration because we do not yet have the function y(x), which we need in order to calculate y’(x). A particular y(x) can be found by solving the Euler-Lagrange equation. Euler’s equation was derived from the calculus of variations, and when solved gives us a function which corresponds to an extremum of the integral. There are several forms of Euler’s equation, and we use this one since it includes derivatives with respect to x and y’
The integrand in our expression for torque is the Lagrangian, L(x, y’). A Lagrangian, generally, can be a function of x, x’, y, y’ and even x’’ or y’’, but for our purpose we drop the explicit mention of all but x and y’ since those do not appear in our integrand.
We mentioned that the form of ds which we use makes no difference to the torque calculation; it does, however, make a difference — in a way — as regards Euler’s equation. If we had chosen the other form of ds (the one which includes x’) we would need to derive (or look up) another form of the equation. The solution to Euler’s equation would be the same, however. Euler’s equation allows for the use of generalized coordinates in the Lagrangian. Also, when writing the Lagrangian we drop the constants that appear in front of the integral since they would “divide out” (a technical mathematical term) and thus play no role in the solution of Euler’s equation. Expanding Euler’s equation, we have
This can be simplified without performing the derivative operations. We are left with
If the derivative of a (non-zero) function is zero, then that function must be a (non-zero) constant. This means that we can write
Now we take the partial derivative of the Lagrangian,
and solve for y’,
or,
We integrate both sides to find y(x) which satisfies Euler’s equation.
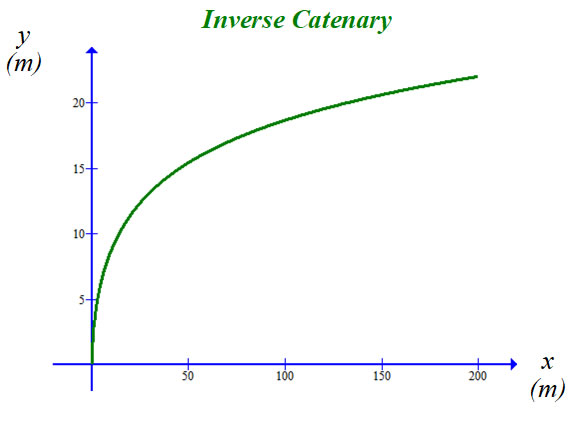
We take note that this is an inverse function. We also remind ourselves that solutions to Euler’s equation produce functions, y(x), which represent an extremum of the integral. In this case the extremum is a minimum, which gives a minimum torque. This means that no other curve between the same endpoints and with the same boundary conditions has a lower torque. Let us graph the function to see what it looks like. |
|
At a glance this does not look like the curve of a kite string, but we press on. To garner an idea of just how much torque is acting on the inverse catenary, we consider the cross product r x dF = r dF sin(φ) = r dF sin(β), where φ is the angle between the vectors and β = 180° - φ. Place the rotational axis at x = a. For small r, the angle β is small; in fact, as r → 0, β → 0, and sin(β) → 0. This means that the contribution (per unit length of string) to the total torque is small for the string near the rotational axis. For large r, that is, as r → ∞, β → 90°, and sin(β) → 1. This means that the contribution (again, per unit length) to the torque is large far from the rotational axis. The constant a determines which particular shape the string takes. For the shape shown in the diagram, we can easily see that a (relatively) large part of this curve is far from the rotational axis and thus the string has, let us say, a fair amount of torque. Nevertheless, this curve represents the minimum torque compared to any other curve with the same boundary conditions and endpoints. This solution to Euler’s equation is an inverse-catenary. Of course its inverse is the catenary, which is open upward, and is the curve that describes the kite string. To make the conversion, all we need do is reflect the curve across the line y = x. In other words, let y → x, and let x → y. We like to reorient the curve with mathematical rigor, just for completeness. To do so, let us invoke the inverse function theorem. Use of this theorem demands that several conditions be met, viz, that on and near the x-values of interest, y must be differentiable, that the differential is not zero, that the inverse of y is defined and be differentiable. If these conditions are met (which we can check later if necessary, but a simple observation of the graph of the curve will answer) then we use an elementary expression of the theorem: the derivative of the inverse is equal to the inverse of the derivative,
Our solution to Euler’s equation gave us
so,
The derivative of y is
Define a new name for the inverse of y(x), which is the curve we are after,
From the inverse function theorem, and the chain rule:
which, rearranged, becomes
Now we want to integrate both sides of that last equation, but we need y’ in terms of y.
Thus,
Integrating both sides and applying appropriate boundary conditions leads to
This is the catenary which describes the kite string. |
|
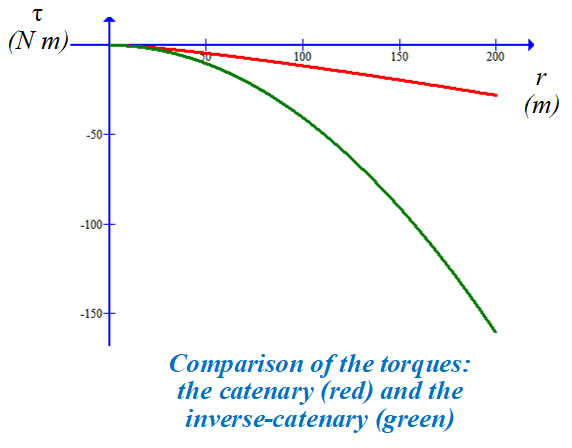
The implication of this analysis is that a rope, thread, wire, chain, cable, string, etc. hanging under its own weight arranges itself under the force of gravity such that the total torque about a rotational axis at the lower end is a minimum. That arrangement is called a catenary curve. This curve represents a minimum torque also— keep in mind that this curve has different boundary conditions and endpoints than the inverse-catenary. We could make a similar argument as above regarding the r and dF vectors. One might say, colloquially, that the closer a segment of the string is to the vertical, the less torque there is on that segment and that a typical kite string is more vertical than horizontal. Meaning only that that this curve has less torque than the inverse-catenary, but they are both minimum extremums for their respective boundary conditions. The Lagrangians for both curves are solutions to Euler’s equation and are thus both minimums. We also note that a slack rope, thread, wire, chain, cable, string, etc. hanging under its own weight with the endpoints at the same horizontal level describes a symmetric catenary, and the total torque is zero if the rotational axis is at the minimum of the curve.
To reiterate: we used the integral
to find that A) the curve of a rope, thread, wire, chain, cable, string, etc. (which is unstretchable, has uniform density, and hangs under its own weight) is the catenary; and B) the catenary curve is the shape of a rope, thread, wire, chain, cable, string, etc. which minimizes the torque on said material (with said characteristics) about a particular rotational axis. A catenary having a minimum torque explains how it became a favorite architectural construct. We have one more interesting observation to make about this derivation of the catenary. It just so happens that the Lagrangian we used above to derive the inverse-catenary (apart from a factor of 2π) is equivalent to a minimum extremum surface-of-revolution integral. Suppose we have some curve and its derivative (used to calculate ds) and we multiply that integral by 2π, then
is the area of a circular ring of circumference 2π x and (two-dimensional) height ds centered on the y-axis. The integration (over either dx or dy) is a rotation about the y-axis which gives the total surface area of the curve and which is a minimum of surface area for the boundary conditions. (For our purpose, remember, we used Euler’s equation to find the curve.) If, instead, we integrate
then we have a minimum area of a proper catenary (open-up, we mean) which is, nevertheless, rotated about the x-axis. But this last is not related to the torque acting on the string and the surface-of-revolution gives us no insight into the physics of the kite string. Our desire to write the torque integral is the reason we used x ds. |
|
Flight Characteristics of a Kite |
|
Torque on a Catenary
We remove from our catenary the offset a distance a along the y-axis and we let θ0 = 0. To calculate the torque about a rotational axis through the origin we begin with
and its derivative,
We also need
which gives us the integral for torque (the negative sign points the torque vector in the – z-direction).
We calculate an indefinite integral and evaluate under the condition: at x = 0, we know that τ = 0. The constant of integration, then, is – ρ g a2.
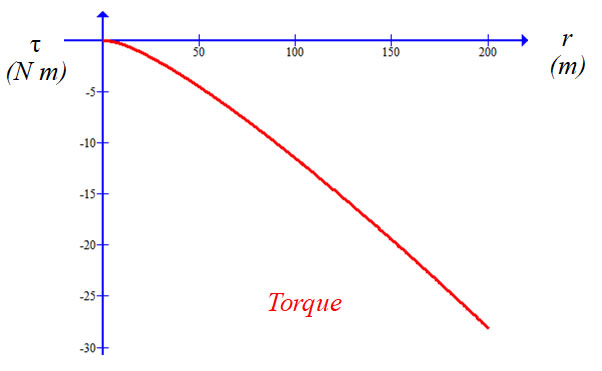
We think that a plot of τ vs. r (and not τ vs. x) gives us more insight. To find r, we write
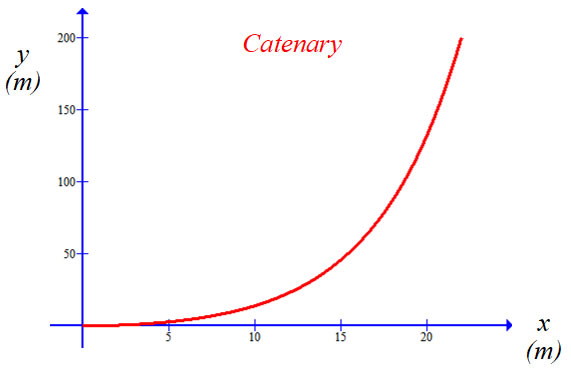
Using x as a parameter, we plot τ along the y-axis and r along the x-axis. For the purpose of illustration, we use a somewhat heavy kite string with ρ = 8.19 x 10-4 kg/m, a = 5 m, and g = 9.81 m/s2. Also, we fly the kite at a rather optimistic y-value of 200 m, which corresponds to an x-value of merely 22 m and an r-value of 201 m. |

|
On the left-hand-side of this equation we prefer transforming to the differential dx. Substituting, we have
We want to integrate over y’ on the right-hand-side,
Now take the indefinite integrals on both sides,
The right-hand-side, we look up: arc-hyperbolic sine! The general form is
Finally, consolidating the constants of integration into one term,
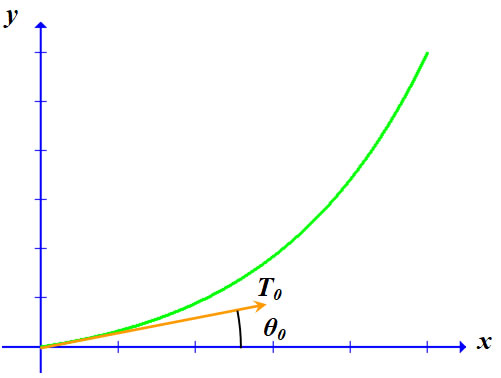
Now a note about boundary conditions. There are an infinite number of catenary curves which fit between a given set of endpoints, the difference being the length of the string. There is only one curve, however, with a horizontal slope at the lower endpoint. For the boundary condition y’(0) = 0, a measurement of the tension at the origin, T(x=0) ≡ T0, is identically equal to Tx, which is both a constant and a most convenient measurement. However, we should consider the possibility that our kite string has a slope at the origin which is not equal to zero. We define, at any point along the string, the angle the string tangent makes with the horizontal as θ and the angle at the origin is θ0. If our kite in flight has a string with a non-zero slope at the kite flyer’s hand, then our force measurement of the tension at the origin would be made tangent to the string at the origin. We would also require a not-impossible measurement of θ0. Since the tension vector is tangent to the string, the boundary condition at the origin would be
where Ty0 = T0 sin(θ0) is the vertical component of the tension at the origin. Back to our equation,
and at x = 0, we have
so,
and
Now integrate; evaluate with the boundary condition y = 0 at x = 0,
This form of integral has the general solution
Thus, the curve
In the case that the slope at the origin is zero, then θ0 = 0 and
Behold the kite string, in general form: |
|
We are not quite finished, however. We want to write a few more equations. The slope of the curve is
From this, we find the angle of the tangent,
The length (here we no longer use the letter L to represent the Lagrangian) of the string, L, is given by
but we have an expression for y’ already, so the integral is
and we invoke a hyperbolic trigonometric identity,
which leads us to
Finally, we want to know the tension in the string at some point x. Recall that the y-component of the tension is given by
and we have,
The tension at a point x is
In terms of measurable quantities, we know that Tx = T0 cos(θ0) and we could always substitute that into our equations as:
but we might want to write Tx in terms of derived quantities by extricating the apparently transcendental Tx from its embedded places in the equations. But it is not transcendental. We begin with expressions
and
Rearranging these two expressions gives us
Using the hyperbolic trigonometric identity which we saw earlier, we now have
and we eventually find an expression for Tx
Let us define R (which has the unit, meter):
and substitute either expression into our equations. Gathering the most useful we have
For the special case θ0 = 0,
and if you do not care for these last expressions, go jump in the lake! . . . er, um, . . . I mean . . . go fly a kite! |
|
The following high precision scientific instruments may be useful in this endeavor:
Surveyor’s rope, 100 meter with 0.1 m increments, for measuring xk and Lk.
Clinometer for measuring α
Fish scale, Chatillon, 15 “KILO”, for measuring T
Triple beam balance, for determining mass
oh, . . . and a kite! |
|
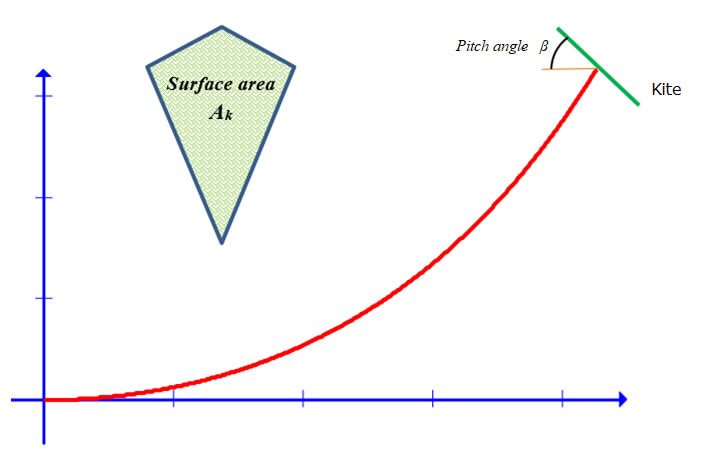
Finally, this analysis could be used by a determined personage to find the dependence of the Lift and Drag on the pitch angle, β, and kite surface area, Ak. An interesting but difficult experiment. |
|
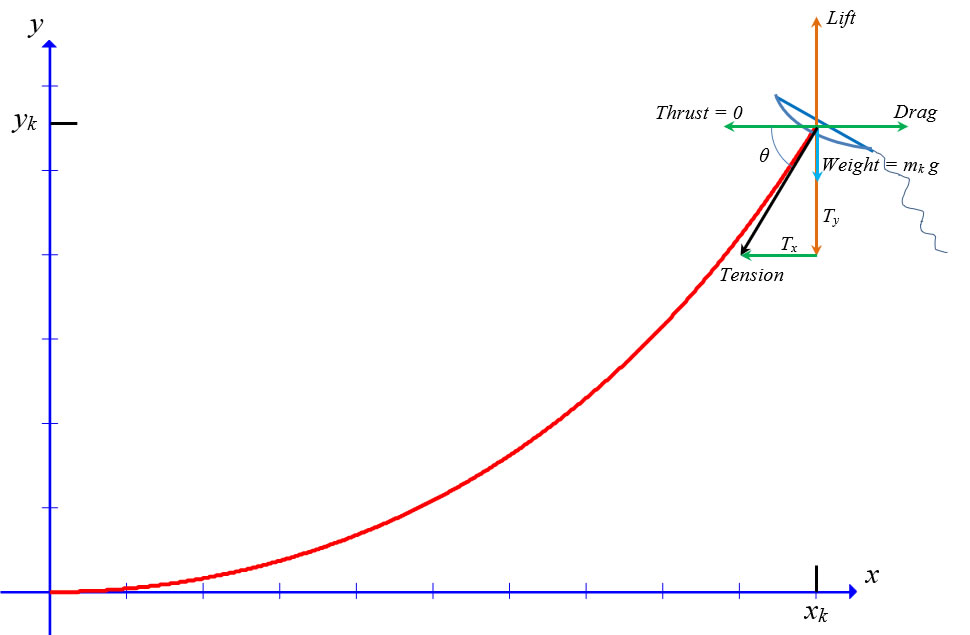
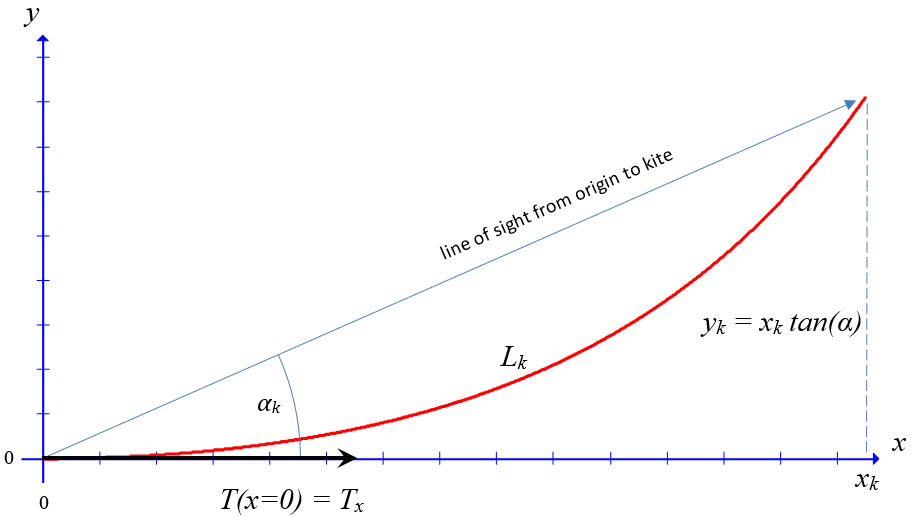
With the kite in this stationary state, we mark the point on the ground directly under the kite as being a distance xk from the origin, and the height of the kite as yk. We make note of the kite string length as Lk. We also notice that if the kite flier at the origin of our coordinate system should hold the string at the minimum point on the catenary, then the tension vector at that point is horizontal. This flight configuration is not always the case, of course. A measurement of the net tension at the origin under these conditions gives us the (constant) value of the x-component of the tension:
We may measure with our clinometer the angle, α, from the horizontal to the line of sight of the kite in order to compare with our calculations.
We may also wish to measure the string length with our surveyor’s rope to compare with our calculation of Lk .
|
|
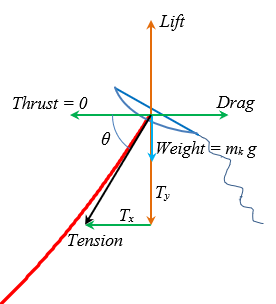
Kites have no thrust. |





|
Bonus
Actual attempt by calculus professor to make a joke:
“This curve, (ex + e-x ) / 2, is known as the catenary.
What should this curve, (ex - e-x ) / 2, be known as, then? The dogenary?” |
|
The End! |
|
If a kite flies in a steady wind and the string length does not change then the kite may be more-or-less stationary, that is, despite being buffeted about a bit by the wind, the kite may remain at a steady height while also remaining over a fixed point on the ground. If this is the case, then the net force acting on the kite is zero. Our aim here is to analyze the flight characteristics of the kite. We now look at the vector forces acting on the kite. From the figure, we see that the Lift force acts upward, and we immediately write the sum of all forces in the y-direction:
where Weight = mk g is the weight of the kite, which has a mass mk. We have an expression for the Lift of the kite,
In the x-direction, the forces give us the Drag
|
|
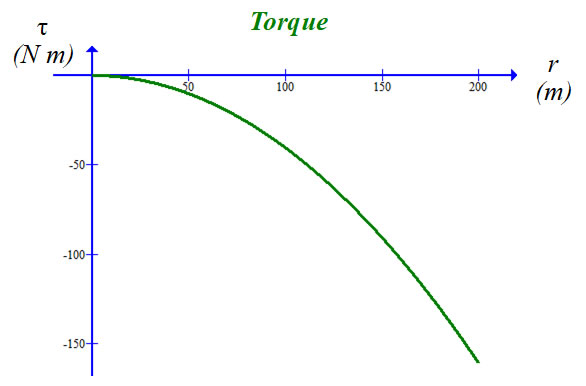
Torque on an Inverse Catenary
Since we discussed the torque on an inverse catenary, why don’t we calculate it? Same routine:
and its derivative
We also need
and the torque is
We eat integrals for breakfast:
The constant of integration is zero. For r, we have
We use the same parameters: ρ = 8.19 x 10-4 kg/m, a = 5 m, g = 9.81 m/s2, maximum y-value = 200 m, maximum x-value = 22 m and an r-value of 201 m. |