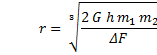|
Black Hole Tidal Force |
|
Astronomy |
|
Tidal Force Caused by Black Hole
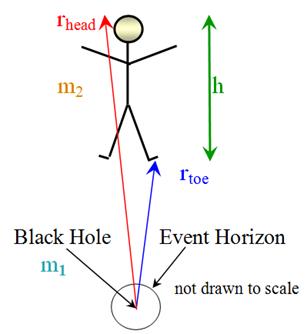
This is how to figure the tidal force on a person due to a black hole.†† The human body will be torn apart if the force differential from head to toe is about ten to twenty times the body weight on earth*.† How closely can an astronaut approach a black hole of, say, 10 solar masses safely out of danger?†
Letís suppose that the astronaut in question has a mass m2 and a height h.† Calculate the force due to gravity exerted by the black hole on the astronaut at the head and at the toe using Newtonís universal law of gravitational attraction**.† The black hole is a singularity in space-time and has no extent in ordinary space no matter how much mass it has.† The force due to gravity at the head points toward the black hole, so the force is
where m1 is the mass of the black hole, rhead is the distance between the black hole and the top of the astronautís head, and G is the universal gravitational constant.† The force due to gravity at the toe, then, is
where rtoe is the distance between the black hole and the astronautís feet.† The tidal force, △F, is the difference in these forces.
†
†
But,
by the definition of height.† Substituting this into the last equation and performing a little algebra gives
The conjecture here is that, at the point of danger, the distance from the black hole to the astronaut likely will be large compared to the astronautís height.† If the astronaut is about two meters tall, then h2 is about 4 meters; make the assumption, then, that 2rheadh>> h2.
If the conjecture is true, then the h2 term can be ignored and dropped from the equation.† This can be checked after the calculation is made; if the conjecture turns out to be wrong Ė then it can be corrected.
Furthermore, that assumption implies
so, ††††††††††††
With this the tidal force becomes
Solve this last equation for rhead.
Take △F to be the average value of 15m2g, where g is the acceleration due to gravity on earth.† Since △F is proportional to m2, the m2 cancels from the equation.† This means that the mass of the astronaut makes no difference in how close the astronaut can approach without danger.
Although the height of the astronaut does matter in the danger point calculation, the assumption that the distance from the black hole to the astronautís head is about the same as the distance to the feet means the subscripts can be dropped; use the notation r for the approximate distance from the black hole to the astronaut at the point of danger.
Use MKS units.† Let Mo be the mass of the sun; for a ten solar mass black hole: †††††††††††† G = 6.67 x 10-11 Nm2/kg2 †††††††††††† m1 = 10. Mo = 10. x 2 x 1030kg = 2.0 x 1031kg †††††††††††† h = 2.0 meters †††††††††††† g = 9.81 m/s2
then ††††††††††††† †††††††††††† ††† = 3.31 x 106 m †††††††††††† ††† = 3.31 x 103 m †††††††††††† †††† or, about 3300 km.
Thus the human body will break up as it nears 3300 kilometers (about 2100 miles).† The event horizon for a black hole of this size is about 30 kilometers, or about 19 miles.† Plenty of time to turn around.
If the astronaut should fall further towards the black hole, because of the force differential the feet will be accelerated at a rate greater than the head.† Thus the hapless astronautóand his space suit, the space ship and everything else in the vicinity, will be stretched like a strand of spaghetti and, if given any angular momentum, will spiral inwards like a cinnamon bun.
*Astronomy Today, E. Chaisson and S. McMillan, 6th ed., Pearson, page 600.†
** These two expressions for gravitational force assume that all of the astronautís mass is concentrated at the head or foot, respectively.
//////////////////////////////////////////////////////////////\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Shortcut for Calculus Fans
In order to find the rate of change of the gravitational force with respect to the location of the astronaut, let r be the distance from the black hole to the astronaut; then the force due to gravity is
The negative sign means that the force at the astronaut points toward the black hole.† Now, the derivative of the force with respect to the astronautís location is
This derivative is equal to the differential ΔF/Δr.† The differential force from head to toe can be found if we let the differential position Δr be the astronautís height, h.
Substitute h for Δr, and solve for r,
Same result as above.
////////////////////////////////////////////////////////////////\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
webpages and EOS image copyright 2016† M† Nealon |